Many distinct fields of application of the theory of cyclostationary time-series analysis are identified on the Home Page, and the number of research papers found by a carefully performed web search is used there as a metric for the apparent level of activity involving cyclostationarity in each of these fields. However, specific research papers are not singled out there as worthy examples. In contrast, the purpose of the present page is to direct readers to a single source where many fine examples are cited.
The research required for this section was recently completed and reported in a new book on cyclostationarity. This book, entitled Cyclostationary Processes and Time Series: Theory, Applications, and Generalizationsand authored by Professor Antonio Napolitano, is the most comprehensive and up-to-date treatment of the entire field of cyclostationarity (including its generalizations), and it is written by today’s foremost developer and chronicler of advances in cyclostationarity. Chapters 9 and 10 include a survey of fields of application of the cyclostationarity paradigm and identify on the order of 100 distinct applications and cite about 500 published papers addressing these applications. A sampling of the application areas identified is given here and includes the pages where this material can be found.
Rather than including here in this section of the website material that would be highly redundant with this up-to-date book, readers are referred to this book via the link [B2].
Another source of applications, which was not available to the author of the above book and which provides an in-depth survey of early work on application of cyclostationarity theory and method to the specialized field of signal interception, is the SSPI Report reproduced below. This survey was written 5 years after the publication of the enabling book [Bk2]. In addition, Page 12.1 includes two concise surveys of communications intelligence technology development based on cyclostationarity exploitation. One of these covers the 10-year period following this 1992 report and the other covers the next 10 years, ending in 2012.
Finally, the reader is referred to page 2.5 where the diversity of problems in statistical inference that can be beneficially addressed using the theory of cyclostationarity is illustrated with eleven subfields of statistical signal processing that are briefly surveyed and for which references to specific applied work are cited and linked to.
With regard to contributions from individual academic institutions that are particularly worthy of recognition, there is the University of Naples Federico II in Italy, which stands out among all universities in the West for the magnitude of its contributions to the development of the theory of cyclostationarity and the associated theory of fraction-of-time probability and their applications, particularly to the study of communications systems. The developments coming out of this Neapolitan academic group, focused on Cyclostationarity, strongly complement those from the seminal group at UC Davis. A prime example is the collaborative work leading to the award-winning comprehensive 2006 survey paper “Cyclostationarity: Half a Century of research”, which is accessible here [JP64].
A capstone of this body of work is the encyclopedic treatise on cyclostationarity written by Professor Antonio Napolitano and published in 2019 [B2], entitled Cyclostationary Processes and Time Series: Theory, Applications, and Generalizations (590 pages). As of this writing (2024), this is the most comprehensive and scholarly treatment of this subject to appear in book form. A key figure in this group, Professor Luigi Paura (master’s thesis advisor of Napolitano), arranged for the WCM to deliver a series of lectures on cyclostationarity shortly after the 1987 publication of his seminal book on this subject, Statistical Spectral Analysis: A Nonprobabilistic Theory. These lectures were delivered at the following leading Italian universities.
Università degli Studi di Napoli “Federico II”
Università degli Studi di Firenze
Università degli Studi di Genova
Alma Mater Studiorum – Università d Bologna
Università degli Studi di Palermo
Faculty and Students of this Neapolitan academic group are listed below. Those with a university affiliation were/are faculty members, and the others were graduate students.
Leopoldo Angrisani – Università di Napoli “Federico II”
Stefano Buzzi – Università di Cassino
Donatella Darsena – Università di Napoli “Federico II”
Valentina de Angelis – Johnson Controls
Filomena Flagiello – Vodafone
Tilde Fusco – ART (Autorité de Régulation des Transports)
Giacinto Gelli – Università di Napoli “Federico II”
Ivan Iudice – CIRA Italian Aerospace
Luciano Izzo – Università di Napoli “Federico II”
Marco Lops – Università di Napoli “Federico II”
Davide Mattera – Università di Napoli “Federico II”
Antonio Napolitano – Università “Parthenope”
Luigi Paura – Università di Napoli “Federico II”
Ivana Perna – Elettronica GmbH,
Giovanni Poggi – Università di Napoli “Federico II”
Arturo Ragozzini – AGCOM
Simone Ricciardelli – ENI
Mario Tanda – Università di Napoli “Federico II”
Manlio Tesauro – Università della Basilicata
Antonia Maria Tulino – Università di Napoli “Federico II”
Michele Vadursi – European Patent Office
Francesco Verde – Università di Napoli “Federico II”
This group is augmented by the following list of researchers who collaborated with Professor Napolitano in the area of cyclostationarity and fraction-of-time probability:
Dominique Dehay, Université Rennes 2, Rennes, France
Kutluyıl Dogançay, University of South Australia, Mawson Lake, Australia
Yaxin Du, Tsinghua University, Shenzhen, China
Anna Dudek, AGH University of Krakow, Krakow, Poland
Piotr Homola, Inst. of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
Julien Le Kernec, University of Glasgow, Glasgow, United Kingdom
Jacek Leskow, American University of Kyiv, Ukraine
Jipeng Li, Shanghai Jiaotong University, Shanghai, China
Bartosz Majewski, AGH University of Krakow, Krakow, Poland
Hernando Ombao, King Abdullah Univ. of Science and Technology, Jeddah, Saudi Arabia
Timofey Shevgunov, Moscow Aviation Institute, Moscow, Russia
Agnieszka Wylomanska, Wrocław University of Science and Technology, Poland
Ran Yu, Tsinghua University, Shenzhen, China
Two graduate schools stand out among all others in terms of the seminal roles they played in the early stages of investigation into the utility of cyclostationarity exploitation for purposes of signals intelligence: the U.S. Naval Postgraduate School (which includes a strong presence by the U.S. Army) and the College of Engineering at the University of California, Davis. The synergistic relationship between the signal processing research groups at these two institutes and a listing of graduate theses are provided on Page 12. Other notable contributors include the U.S. Air Force Institute of Technology, which shows about 20 cyclostationarity-based theses/dissertations here. In addition to the role played by these military schools, the research offices of the Army, Navy, and Air Force, as well as various military research laboratories have played a major role in funding cyclostationarity research and development at numerous public academic institutions and research corporations. See, for example, the partial list below of participants at the first cyclostationarity workshop. Also, corresponding military offices and R & D Labs among US Allies around the World have made notable contributions to advances in this field. US Allies include Canada, France, Germany, Italy, Japan, the United Kingdom, the United States and the European Union, Turkey, Spain, Poland, Norway, North Macedonia, Netherlands, Luxembourg, Greece, Denmark, Czech Rep, Belgium, India, Japan, Australia, Sweden, Finland, Ireland, Israel, New Zealand, Mexico, Ukraine; in short, all NATO, G7 and Quad Group member states are US Allies.
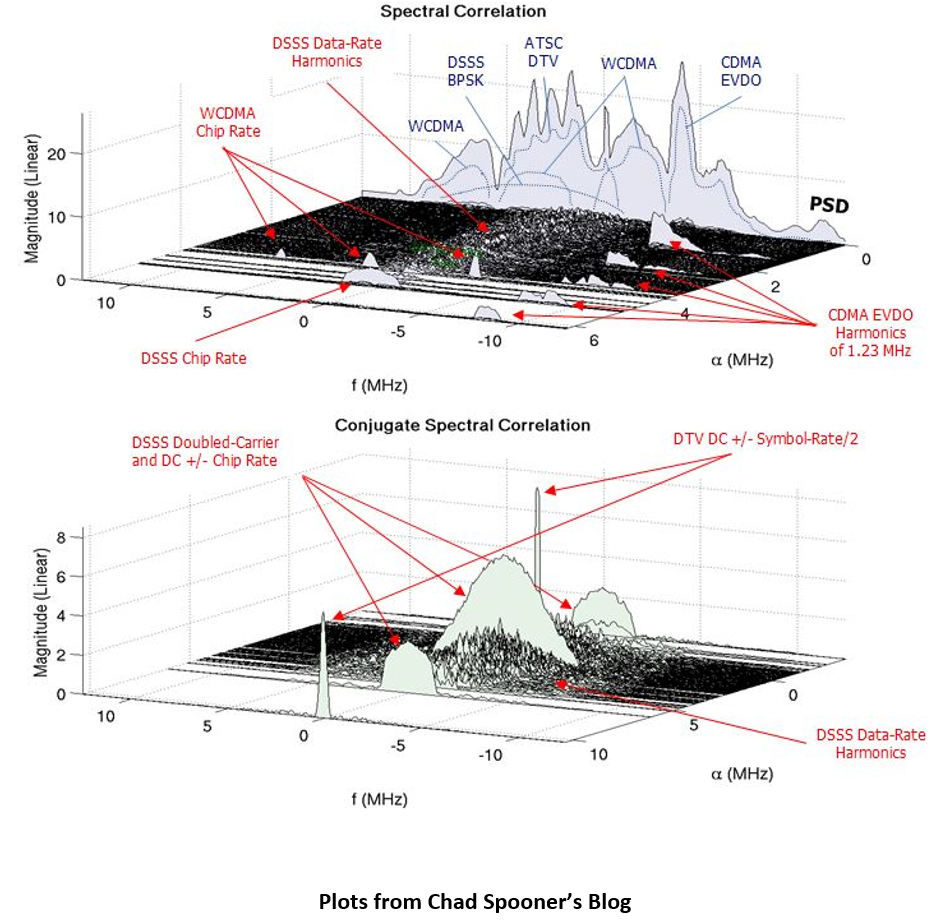
For practitioners of cyclostationary signal processing, some of the nitty-gritty details encountered in implementing algorithms are addressed at this blog. A graphic example of the complexity of the spectrum of the sum of individual signals contained in some radio signal environments is given by Chad Spooner at his blog here and is copied below. This is a plot of the magnitude of the measured spectral correlation function (cyclic spectrum) above the plane with coordinates f (f = frequency = location such as midpoint or left end or right end of the interval between the center frequencies of the two narrowband components whose correlation is being displayed) and alpha (alpha = cycle frequency = frequency separation of these two narrowband components). Observe that the plot above the alpha = 0 line in the plane is the spectral density of time-averaged power (power spectral density = PSD) of this mix of signals. It can be seen that the individual contributions to the PSD from each signal in the environment cannot be distinguished very well. However, the contributions to spectral correlation from individual signals is easily identified because these occur above lines in the plane that are distinct, because the cycle frequencies of the individual signals are distinct. This illustrates the separability of spectral correlation features of signals that overlap in the PSD.

In the 2-decade period following the brief period covered by the above 1992 overview report, the WCM’s R&D company SSPI continued its development of theory and method for signals intelligence until that company closed following the sale of its intellectual property to Lockheed Martin in 2011. Very little of the results of that R&D has been published and it remains, another decade later, classified by the US government. Nevertheless, applications of cyclostationarity outside the field of signals intelligence during those thirty years has seen tremendous growth.For the sake of completeness, this page is concluded with a presentation of all four tables of results from the internet search that appeared in the original publication [JP65] from which the single table presented herein on the Home Page was taken. These search results establish the fact that cyclostationarity concepts, theory, and method have permeated essentially every field of science and engineering, as predicted by the WCM upon completion of his seminal book [Bk2] published in 1987. From this survey data, one must conclude that the subject of this website has—since the publication of [Bk2]—become a major new subfield, within the classical field of statistical Statistical | adjective Of or having to do with Statistics, which are summary descriptionscomputed from finite sets of empirical data; not necessarily related to probability. time-series analysis. The importance of this subfield is not dependent on technology and will only increase in importance in the foreseeable future. This fact justifies this educational website.
Researchers seeking insight into theory and method for the following topics should benefit from the sources cited above: adaptive filtering algorithms, adaptive equalization algorithms, adaptive noise reduction algorithms, least mean square (LMS), recursive least squares (RLS), normalized least mean squares (NLMS), stochastic gradient descent (SGD), channel identification, channel equalization, blind equalization, blind channel equalization, weak signals, weak signal detection, weak communications signals, detection of weak communications signals, adaptive spatial filtering algorithms, emitter location, RF geolocation, radio source location, radio direction finding, triangulation, time difference of arrival estimation, frequency difference of arrival, communications signal classification and modulation classification, time series prediction and forecasting.
The web search results shown below were obtained using Google Scholar. This search was based on 45 nearly-distinct applications areas in science and engineering, and the search terms were chosen to yield only results involving exploitation of cyclicity in time-series data. By “nearly distinct”, it is meant that the search terms were also selected to minimize redundancy (multiple search application areas producing the same “hits”).As shown in Table 1, the search found about 136 thousand published research papers. Additional web search results are shown in Table 2. This search was based on 24 partially redundant general subject areas and it found 238 thousand published research papers.

To complement the historical perspective on applications of cyclostationarity provided in the 1992 Technical Report included on this page just prior to the above four tables, two documents prepared just following the 1992 Workshop are included below. The first identifies about half of the research laboratories that sent representatives to participate in this workshop and the second is a 1992 press release prepared by the University of California, Davis.