2. Learning About Cyclostationarity

FOREWORD

A good deal of our statistical theory, although it is mathematical in nature, originated not in mathematics but in problems of astronomy, geomagnetism and meteorology: examples of fruitful problems in these subjects have included the clustering of stars, also galaxies, on the celestial sphere, tidal analysis, the correlation of fluctuations of the Earth’s magnetic field with other solar-terrestrial effects, and the determination of seasonal variations and climatic trends from weather data. All three of these fields are observational. Great figures of the past, such as C. F. Gauss (1777—1855) (who worked with both astronomical and geomagnetic data, and discovered the method of least square fitting of data, the normal error distribution, and the Fast Fourier Transform algorithm), have worked on observational data analysis and have contributed much to our body of knowledge on time series and randomness.

Much other theory has come from gambling, gunnery, and agricultural research, fields that are experimental. Measurements of the fall of shot on a firing range will reveal a pattern that can be regarded as a sample from a normal distribution in two dimensions, together with whatever bias is imposed by pointing and aiming, the wind, air temperature, atmospheric pressure and Earth rotation. The deterministic part of any one of these influences may be characterized with further precision by further firing tests. In the experimental sciences, as well as in the observational, great names associated with the foundations of statistics and probability also come to mind.

Experimental subjects are traditionally distinguished from observational ones by the property that conditions are under the control of the experimenter. The design of experiments leads the experimenter to the idea of an ensemble, or random process, an abstract probabilistic creation illustrated by the bottomless barrel of well-mixed marbles that is introduced in elementary probability courses. A characteristic feature of the contents of such a barrel is that we know in advance how many marbles there are of each color, because it is we who put them in; thus, a sample set that is withdrawn after stirring must be compatible with the known mix.

The observational situation is quite unlike this. Our knowledge of what is in the barrel, or of what Nature has in store for us, is to be deduced from what has been observed to come out of the barrel, to date. The probability distribution, rather than being a given, is in fact to be intuited from experience. The vital stage of connecting the world of experience to the different world of conventional probability theory may be glossed over when foreknowledge of the barrel and its contents — a probabilistic model — are posited as a point of departure. Many experimental situations are like this observational one.

The theory of signal processing, as it has developed in electrical and electronics engineering, leans heavily toward the random process, defined in terms of probability distributions applicable to ensembles of sample signal waveforms. But many students who are adept at the useful mathematical techniques of the probabilistic approach and quite at home with joint probability distributions are unable to make even a rough drawing of the underlying sample waveforms. The idea that the sample waveforms are the deterministic quantities being modeled somehow seems to get lost.

When we examine the pattern of fall of shot from a gun, or the pattern of bullet holes in a target made by firing from a rifle clamped in a vise, the distribution can be characterized by its measurable centroid and second moments or other spread parameters. While such a pattern is necessarily discrete, and never much like a normal distribution, we have been taught to picture the pattern as a sample from an infinite ensemble of such patterns; from this point of view the pattern will of course be compatible with the adopted parent population, as with the marbles. In this probabilistic approach, to simplify mathematical discussion, one begins with a model, or specification of the continuous probability distribution from which each sample is supposed to be drawn. Although this probability distribution is not known, one is comforted by the assurance that it is potentially approachable by expenditure of more ammunition. But in fact it is not.

The assumption of randomness is an expression of ignorance. Progress means the identification of systematic effects which, taken as a whole, may initially give the appearance of randomness or unpredictability. Continuing to fire at the target on a rifle range will not refine the probability distribution currently in use but will reveal, to a sufficiently astute planner of experiments, that air temperature, for example, has a determinate effect which was always present but was previously accepted as stochastic. After measurement, to appropriate precision, temperature may be allowed for. Then a new probability model may be constructed to cover the effects that remain unpredictable.

Many authors have been troubled by the standard information theory approach via the random process or probability distribution because it seems to put the cart before the horse. Some sample parameters such as mean amplitudes or powers, mean durations and variances may be known, to precision of measurement, but if we are to go beyond pure mathematical deduction and make advances in the realm of phenomena, theory should start from the data. To do otherwise risks failure to discover that which is not built into the model. Estimating the magnitude of an earthquake from seismograms, assessing a stress-test cardiogram, or the pollutant in a stormwater drain, are typical exercises where noise, systematic or random, is to be fought against. Problems on the forefront of development are often ones where the probability distributions of neither signal nor noise is known; and such distributions may be essentially unknowable because repetition is impossible. Thus, any account of measurement, data processing, and interpretation of data that is restricted to probabilistic models leaves something to be desired.

The techniques used in actual research with real data do not loom large in courses in probability. Professor Gardner’s book demonstrates a consistent approach from data, those things which in fact are given, and shows that analysis need not proceed from assumed probability distributions or random processes. This is a healthy approach and one that can be recommended to any reader.

Ronald N. Bracewell
Stanford, California

PREFACE

This book grew out of an enlightening discovery I made a few years ago, as a result of a long-term attempt to strengthen the tenuous conceptual link between the abstract probabilistic theory of cyclostationary stochastic processes and empirical methods of signal processing that accommodate or exploit periodicity in random data. After a period of unsatisfactory progress toward using the concept of ergodicity¹ to strengthen this link, it occurred to me (perhaps wishfully) that the abstraction of the probabilistic framework of the theory might not be necessary. As a first step in pursuing this idea, I set out to clarify for myself the extent to which the probabilistic framework is needed to explain various well-known concepts and methods in the theory of stationary stochastic processes, especially spectral analysis theory. To my surprise, I discovered that all the concepts and methods of empirical spectral analysis can be explained in a more straightforward fashion in terms of a deterministic theory, that is, a theory based on time-averages of a single time-series rather than ensemble-averages of hypothetical random samples from an abstract probabilistic model. To be more specific, I found that the fundamental concepts and methods of empirical spectral analysis can be explained without use of probability calculus or the concept of probability and that probability calculus, which is indeed useful for quantification of the notion of degree of randomness or variability, can be based on time-averages of a single time-series without any use of the concept or theory of a stochastic process defined on an abstract probability space. This seemed to be of such fundamental importance for practicing engineers and scientists and so intuitively satisfying that I felt it must already be in the literature.

To put my discovery in perspective, I became a student of the history of the subject. I found that the apparent present-day complacence with the abstraction of the probabilistic theory of stochastic processes, introduced by A. N. Kolmogorov in 1941, has been the trend for about 40 years (as of 1985). Nevertheless, I found also that many probabilists throughout this period, including Kolmogorov himself, have felt that the concept of randomness should be defined as directly as possible, and that from this standpoint it seems artificial to conceive of a time-series as a sample of a stochastic process. (The first notable attempt to set up the probability calculus more directly was the theory of Collectives introduced by Von Mises in 1919; the mathematical development of such alternative approaches is traced by P. R. Masani [Masani 1979].) In the engineering literature, I found that in the early 1960s two writers, D. G. Brennan [Brennan 1961] and E. M. Hofstetter [Hofstetter 1964], had made notable efforts to explain that much of the theory of stationary time-series need not be based on the abstract probabilistic theory of stochastic processes and then linked with empirical method only through the abstract concept of ergodicity, but rather that a probabilistic theory based directly on time-averages will suffice; however, they did not pursue the idea that a theory of empirical spectral analysis can be developed without any use of probability. Similarly, the more recent book by D. R. Brillinger on time-series [Brillinger 1975] briefly explains precisely how the probabilistic theory of stationary time-series can be based on time-averages, but it develops the theory of empirical spectral analysis entirely within the probabilistic framework. Likewise, the early engineering book by R. B. Blackman and J. W. Tukey [Blackman and Tukey 1958] on spectral analysis defines an idealized spectrum in terms of time-averages but then carries out all analysis of measurement techniques within the probabilistic framework of stochastic processes. In the face of this 40-year trend, I was perplexed to find that the one most profound and influential work in the entire history of the subject of empirical spectral analysis, Norbert Wiener’s Generalized Harmonic Analysis, written in 1930 [Wiener 1930], was entirely devoid of probability theory; and yet I found only one book written since then for engineers or scientists that provides more than a brief mention of Wiener’s deterministic theory. All other such books that I found emphasize the probabilistic theory of A. N. Kolmogorov usually to the complete exclusion of Wiener’s deterministic theory. This one book was written by a close friend and colleague of Wiener’s, Y. W. Lee, in 1960 [Lee 1960]. Some explanation of this apparent historical anomaly is given by P. R. Masani in his recent commentary on Wiener’s Generalized Harmonic Analysis [Masani 1979]: “The quick appearance of the Birkhoff ergodic theorem and the Kolmogorov theory of stochastic processes after the publication of Wiener’s Generalized Harmonic Analysis created an intellectual climate favoring stochastic analysis rather than generalized harmonic analysis.” But Masani goes on to explain that the current opinion, that Wiener’s 1930 memoir [Wiener 1930] marks the culmination of generalized harmonic analysis and its supersession by the more advanced theories of stochastic processes, is questionable on several counts, and he states that the “integrity and wisdom” in the attitude expressed in the early 1960s by Kolmogorov suggesting a possible return to the ideas of Von Mises “. . . should point the way toward the future. Side by side with the vigorous pursuit of the theory of stochastic processes, must coexist a more direct process-free [deterministic] inquiry of randomness of different classes of functions.”

As a result of my discovery and my newly gained historical perspective, I felt compelled to write a book that would have the same goals, in principle, as many existing books on spectral analysis—to present a general theory and methodology for empirical spectral analysis—but that would present a more relevant and palatable (for many applications) deterministic theory following Wiener’s original approach rather than the conventional probabilistic theory. As the book developed, I continued to wonder about the apparent fact that no one in the 50 years (as of 1985) since Wiener’s memoir had considered such a project worthy enough to pursue. However, as I continued to search the literature, I found that one writer, J. Kampé de Fériet. did make some progress along these lines in a tutorial paper [Kampé de Fériet 1954], and other authors have contributed to development of deterministic theories of related subjects in time-series analysis, such as linear prediction and extrapolation [Wold 1948], [Finch 1969], [Fine 1970]. Furthermore, as the book progressed and I observed the favorable reactions of my students and colleagues, my conviction grew to the point that I am now convinced that it is generally beneficial for students of the subject of empirical spectral analysis to study the deterministic theory before studying the more abstract probabilistic theory.

When I had completed most of the development for a book on a deterministic theory of empirical spectral analysis of stationary time-series, I was then able to return to the original project of presenting the results of my research work on cyclostationary time-series but within a nonprobabilistic framework. Once I started, it quickly became apparent that I was able to conceptualize intuitions, hunches, conjectures, and so forth far more clearly than before when I was laboring within the probabilistic framework. The original relatively fragmented research results on cyclostationary stochastic processes rapidly grew into a comprehensive theory of random time-series from periodic phenomena that is every bit as satisfying as the theory of random time-series from constant phenomena (stationary time-series) and is even richer. This theory, which brings to light the fundamental role played by spectral correlation in the study of periodic phenomena, is presented in Part II.

Part I of this book is intended to serve as both a graduate-level textbook and a technical reference. The only prerequisite is an introductory course on Fourier analysis. However, some prior exposure to probability would be helpful for Section B in Chapter 5 and Section A in Chapter 15. The body of the text in Part I presents a thorough development of fundamental concepts and results in the theory of statistical spectral analysis of empirical time-series from constant phenomena, and a brief overview is given at the end of Chapter 1. Various supplements that expand on topics that are in themselves important or at least illustrative but that are not essential to the foundation and framework of the theory, are included in appendices and exercises at the ends of chapters.

Part II of this book, like Part I, is intended to serve as both textbook and reference, and the same unifying philosophical framework developed in Part I is used in Part II. However, unlike Part I, the majority of concepts and results presented in Part II are new. Because of the novelty of this material, a brief preview is given in the Introduction to Part II. The only prerequisite for Part II is Part I.

The focus in this book is on fundamental concepts, analytical techniques. and basic empirical methods. In order to maintain a smooth flow of thought in the development and presentation of concepts that steadily build on one another, various derivations and proofs are omitted from the text proper, and are put into the exercises, which include detailed hints and outlines of solution approaches. Depending on students’ background, instructors can either assign these as homework exercises, or present them in the lectures. Because the treatment of experimental design and applications is brief and is also relegated to the exercises and concise appendices, some readers might desire supplements on these topics.

===============

¹ Ergodicity is the property of a mathematical model for an infinite set of time-series that guarantees that an ensemble average over the infinite set will equal an infinite time average over one member of the set.

REFERENCES

BLACKMAN, R. B. and J, W. TUKEY. 1958. The Measurement of Power Spectra. New York: American Telephone and Telegraph Co.
BRENNAN, D. G. 1961. Probability theory in communication system engineering, Chapter 2 in Communication System Theory. Ed. E. J. Baghdady, New York: McGraw-Hill.
BRILLINGER, D. R. 1975. Time Series. New York: Holt, Rinehart and Winston.
FINCH, P. D. 1969. Linear least squares prediction in non-stochastic time-series. Advances in Applied Prob. 1:111—22.
FINE, T. L. 1970. Extrapolation when very little is known about the source. Information and Control. 16:33 1—359.
HOFSTETTER, E. M. 1964. Random processes. Chapter 3 in The Mathematics of Physics and Chemistry, vol. 11. Ed. H. Margenau and G. M. Murphy. Princeton, N.J.: D. Van Nostrand Co.
KAMPÉ DE FÉRIET, J. 1954. Introduction to the statistical theory of turbulence. I and 11. J. Soc. Indust. Appl. Math. 2, Nos. I and 3:1—9 and 143—174.
LEE, Y. W. 1960. Statistical Theory of Communication. New York: John Wiley & Sons.
MASANI, P. R. 1979. “Commentary on the memoir on generalized harmonic analysis.” pp. 333—379 in Norbert Wiener: Collected Works, Volume II. Cambridge. Mass.: Massachusetts Institute of Technology.
WIENER, N. 1930. Generalized harmonic analysis. Acta Mathematika. 55:117—258.
WOLD, H. O. A. 1948. On prediction in stationary time-series. Annals of Math Stat. 19:558—567.

William A. Gardner

Part I, CONSTANT PHENOMENA

INTRODUCTION

The subject of Part I is the statistical spectral analysis of empirical time-series. The term empirical indicates that the time-series represents data from a physical phenomenon; the term spectral analysis denotes decomposition of the time-series into sine wave components; and the term statistical indicates that the squared magnitude of each measured or computed sine wave component, or the product of pairs of such components, is averaged to reduce random effects in the data that mask the spectral characteristics of the phenomenon under study. The purpose of Part I is to present a comprehensive deterministic theory of statistical spectral analysis and thereby to show that contrary to popular belief, the theoretical foundations of this subject need not be based on probabilistic concepts. The motivation for Part I is that for many applications the conceptual gap between practice and the deterministic theory presented herein is narrower and thus easier to bridge than is the conceptual gap between practice and the more abstract probabilistic theory. Nevertheless, probabilistic concepts are not ignored. A means for obtaining probabilistic interpretations of the deterministic theory is developed in terms of fraction-of-time distributions, and ensemble averages are occasionally discussed.

A few words about the terminology used are in order. Although the terms statistical and probabilistic are used by many as if they were synonymous, their meanings are quite distinct. According to the Oxford English Dictionary, statistical means nothing more than “consisting of or founded on collections of numerical facts”. Therefore, an average of a collection of spectra is a statistical spectrum. And this has nothing to do with probability. Thus, there is nothing contradictory in the notion of a deterministic or non-probabilistic theory of statistical spectral analysis. (An interesting discussion of variations in usage of the term statistical is given in Comparative Statistical Inference by V. Barnett [Barnett 1973]). The term deterministic is used here as it is commonly used, as a synonym for non-probabilistic. Nevertheless, the reader should be forewarned that the elements of the non-probabilistic theory presented herein are defined by infinite limits of time averages and are therefore no more deterministic in practice than are the elements of the probabilistic theory. (In mathematics, the deterministic and probabilistic theories referred to herein are sometimes called the functional and stochastic theories, respectively.) The term random is often taken as an implication of an underlying probabilistic model. But in this book, the term is used in its broader sense to denote nothing more than the vague notion of erratic unpredictable behavior.

Chapter 1, INTRODUCTION TO SPECTRAL ANALYSIS

This introductory chapter sets the stage for the in-depth study of spectral analysis taken up in the following chapters by explaining objectives and motives, answering some basic questions about the nature and uses of spectral analysis, and establishing a historical perspective on the subject.

A. OBJECTIVES AND MOTIVES

A premise of this book is that the way engineers and scientists are commonly taught to think about empirical statistical spectral analysis of time-series data is fundamentally inappropriate for many applications—maybe even most. The essence of the subject is not really as abstruse as it appears to be from what has become the conventional point of view. The problem is that the subject has been imbedded in the abstract probabilistic framework of stochastic processes, and this abstraction impedes conceptualization of the fundamental principles of empirical statistical spectral analysis. To circumvent this artificial conceptual complication, the probabilistic theory of statistical spectral analysis should be taught to engineers and scientists only after they have learned the fundamental deterministic principles—both qualitative and quantitative. For example, one should first learn 1) when and why sine wave analysis of time-series is appropriate, 2) how and why temporal and spectral resolution interact, 3) why statistical (averaged) spectra are of interest, and 4) what the various methods for measuring and computing statistical spectra are and how they are related. One should also learn 5) how simultaneously to control the spectral and temporal resolution and the degree of randomness (reliability) of a statistical spectrum. All this can be accomplished in a non-superficial way without reference to the probabilistic theory of stochastic processes.

The concept of a deterministic theory of statistical spectral analysis is not new. Much deterministic theory was developed prior to and after the infusion, beginning in the 1930s, of probabilistic concepts into the field of time-series analysis. The most fundamental concept underlying present-day theory of statistical spectral analysis is the concept of an ideal spectrum, and the primary objective of statistical spectral analysis is to estimate the ideal spectrum using a finite amount of data. The first theory to introduce the concept of an ideal spectrum is Norbert Wiener’s theory of generalized harmonic analysis [Wiener 1930], and this theory is deterministic. Later, Joseph Kampé de Fériet presented a deterministic theory of statistical spectral analysis that ties Wiener’s theory more closely to the empirical reality of finite-length time-series [Kampé de Fériet 1954]. But the very great majority of treatments in the ensuing 30 years consider only probabilistic theory of statistical spectral analysis that is based on the use of stochastic process models of time functions, although a few authors do briefly mention the dual deterministic theory (e.g., [Koopmans 1974; Brillinger 1976]).

The primary objective of Part I of this book is to adopt the deterministic viewpoint of Wiener and Kampé de Fériet and show that a comprehensive deterministic theory of statistical spectral analysis, which for many applications relates more directly to empirical reality than does its more popular probabilistic counterpart based on stochastic processes, can be developed. A secondary objective of Part I is to adopt the empirical viewpoint of Donald G. Brennan [Brennan 1961] and Edward M. Hofstetter [Hofstetter 1964], from which they develop an objective probabilistic theory of stationary random processes based on fraction-of-time distributions, and show that probability theory can be applied to the deterministic theory of statistical spectral analysis without introducing the more abstract mathematical model of empirical reality based on the axiomatic or subjective probabilistic theory of stochastic processes. This can be interpreted as an exploitation of Herman O. A. Wold’s isomorphism between an empirical time-series and a probabilistic model of a stationary stochastic process. As explained below in Section B, this isomorphism is constructed by defining the ensemble, upon which the probabilistic theory of time functions is based, to be the set of all time-translated versions of a single function of time—the ensemble generator—and it is responsible for the duality between probabilistic (ensemble-average) and deterministic (time-average) theories of time-series [Wold 1948] [Gardner 1985]. Moreover, the excuse generally offered for adopting a stochastic process model when it is admitted that it is time averages, not ensemble averages, that are of interest in practice is to carelessly assume that the stochastic process is ergodic (an even more abstract concept), in which case time-averages converge to ensemble averages—a result typically presented to students as magic; what is not generally mentioned (and probably rarely even recognized by instructors) is that assuming ergodicity is tantamount to assuming the ensemble is (with probability equal to one) simply the collection of all time-translated versions of a single time function. Thus, the whole exercise of abandoning the more straightforward fraction-of-time probabilistic model in favor of the abstract stochastic process model is all for naught. So why drag our students through this silly exercise that is bound to serve no purpose other than to confuse them, especially given that the truth about all this presented here is essentially never revealed to the student.

There are two motives for Part I of this book. The first is to stimulate a reassessment of the way engineers and scientists are today, evidently exclusively, taught to think about statistical spectral analysis by showing that probability theory need not play a primary role. The second motive is to pave the way for introducing a new theory and methodology for statistical spectral analysis of random data from periodically time-variant phenomena, which is presented in Part II. The fact that this new theory and methodology, which unifies various emerging—as well as long-established—time-series analysis concepts and techniques, is most transparent when built on the foundation of the deterministic theory developed in Part I is additional testimony that probability theory need not play a primary role in statistical spectral analysis.

The book, although concise, is tutorial and is intended to be comprehensible by graduate students and professionals in engineering, science, mathematics, and statistics. The accomplishments of the book should be appreciated most by those who have studied statistical spectral analysis in terms of the popular probabilistic theory and have struggled to bridge the conceptual gaps between this abstract theory and empirical reality.

B. ORIENTATION

1. What is Spectral Analysis?

Spectral analysis of functions is used for solving a wide variety of practical problems encountered by engineers and scientists in nearly every field of engineering and science. The functions of primary interest in most fields involving data analysis are temporal or spatial waveforms or discrete sequences of numbers. The most basic purpose of spectral analysis is to represent a function by a sum of weighted sinusoidal functions called spectral components; that is, the purpose is to decompose (analyze) a function into these spectral components. The weighting function in the decomposition is a density of spectral components. This spectral density is also called a spectrum¹. The reason for representing a function by its spectrum is that the spectrum can be an efficient, convenient, and often revealing description of the function.

As an example of the use of spectral representation of temporal waveforms in the field of signal processing, consider the signal extraction problem of extracting an information-bearing signal from corrupted (noisy) measurements. In many situations, the spectrum of the signal differs substantially from the spectrum of the noise. For example, the noise might have more high-frequency content; hence, the technique of spectral filtering can be used to attenuate the noise while leaving the signal intact. Another example is the data-compression problem of using coding to compress the amount of data used to represent information for the purpose of efficient storage or transmission. In many situations, the information contained in a complex temporal waveform (e.g., a speech segment) can be coded more efficiently in terms of the spectrum.

There are two types of spectral representations. The more elementary of the two shall be referred to as simply the spectrum, and the other shall be referred to as the statistical spectrum. The term statistical indicates that averaging or smoothing is used to reduce random effects in the data that mask the spectral characteristics of the phenomenon under study. For time-functions, the spectrum is obtained from an invertible transformation from a time-domain description of a function, , to a frequency-domain description, or more generally to a joint time- and frequency-domain description. The (complex) spectrum of a segment of data of length centered at time and evaluated at frequency is

(1)  

for which . Because of the invertibility of this transformation, a function can be recovered from its spectrum,

(2)  

In contrast to this, a statistical spectrum involves a magnitude-extraction operation that is not invertible followed by an averaging or smoothing operation. For example, the statistical spectrum

(3)  

is obtained from the normalized squared magnitude spectrum

(4)  

followed by a temporal smoothing operation. Thus, a statistical spectrum is a summary description of a function from which the function cannot be recovered. Therefore, although the spectrum is useful for both signal extraction and data compression, the statistical spectrum is not directly useful for either. It is, however, quite useful indirectly for analysis, design, and adaptation of schemes for signal extraction and data compression. It is also useful for forecasting or prediction and more directly for other signal-processing tasks such as 1) the modeling and system-identification problems of determining the characteristics of a system from measurements on it, such as its response to excitation, and 2) decision problems, such as the signal-detection problem of detecting the presence of a signal buried in noise. As a matter of fact, the problem of detecting hidden periodicities in random data motivated the earliest work in the development of spectral analysis, as discussed in Section D below.

Statistical spectral analysis has diverse applications in areas such as mechanical vibrations, acoustics, speech, communications, radar, sonar, ultrasonics, optics, astronomy, meteorology, oceanography, geophysics, economics, biomedicine, and many other areas. To be more specific, let us briefly consider a few applications. Spectral analysis is used to characterize various signal sources. For example, the spectral purity of a sine wave source (oscillator) is determined by measuring the amounts of harmonics from distortion due, for example, to nonlinear effects in the oscillator and also by measuring the spectral content close in to the fundamental frequency of the oscillator, which is due to random phase noise. Also, the study of modulation and coding of sine wave carrier signals and pulse-train signals for communications, telemetry, radar, and sonar employs spectral analysis as a fundamental tool, as do surveillance systems that must detect and identify modulated and coded signals in a noisy environment. Spectral analysis of the response of electrical networks and components such as amplifiers to both sine wave and random-noise excitation is used to measure various properties such as nonlinear distortion, rejection of unwanted components, such as power-supply components and common-mode components at the inputs of differential amplifiers, and the characteristics of filters, such as center frequencies, bandwidths, pass-band ripple, and stop-band rejection. Similarly, spectral analysis is used to study the magnitude and phase characteristics of the transfer functions as well as nonlinear distortion of various electrical, mechanical, and other systems, including loudspeakers, communication channels and modems (modulator-demodulators), and magnetic tape recorders in which variations in tape motion introduce signal distortions. In the monitoring and diagnosis of rotating machinery, spectral analysis is used to characterize random vibration patterns that result from wear and damage that cause imbalances. Also, structural analysis of physical systems such as aircraft and other vehicles employs spectral analysis of vibrational response to random excitation to identify natural modes of vibration (resonances). In the study of natural phenomena such as weather and the behavior of wildlife and fisheries populations, the problem of identifying cause-effect relationships is attacked using techniques of spectral analysis. Various physical theories are developed with the assistance of spectral analysis, for example, in studies of atmospheric turbulence and undersea acoustical propagation. In various fields of endeavor involving large, complex systems such as economics, spectral analysis is used in fitting models to time-series for several purposes, such as simulation and forecasting. As might be surmised from this sampling of applications, the techniques of spectral analysis permeate nearly every field of science and of engineering.

Spectral analysis applies to both continuous-time functions, called waveforms, and discrete-time functions, called sampled data. Other terms are commonly used also; for example, the terms data and time-series are each used for both continuous-time and discrete-time functions. Since the great majority of data sources are continuous-time phenomena, continuous-time data are focused on in this book, because an important objective is to maintain a close tie between theory and empirical reality. Furthermore, since optical technology has emerged as a new frontier in signal processing and optical quantities vary continuously in time and space, this focus on continuous time data is well suited to upcoming technological developments. Nevertheless, since some of the most economical implementations of spectrum analyzers and many of the newly emerging parametric methods of spectral analysis operate with discrete time and discrete frequency and since some data are available only in discrete form, discrete-time and discrete-frequency methods also are described.

===============

¹ The term spectrum, which derives from the Latin for image, was originally introduced by Sir Isaac Newton (see [Robinson 1982]).

2. Why Analyze Waveforms Into Sinewave Components?²

The primary reason why sinewaves are especially appropriate components with which to analyze waveforms is our preoccupation with convolutions of time series with the kernels (impulse-response functions) of linear time-invariant (LTI) transformations, which we often call filters. A secondary reason why statistical (time-averaged) analysis into sinewave components is especially appropriate is our preoccupation with time-invariant phenomena (data sources). To be specific, a transformation of a waveform into another waveform, say , is an LTI transformation if and only if there exists a weighting function (here assumed to be absolutely integrable in the generalized sense, which accommodates Dirac deltas) such that is the convolution (denoted by ) of with :

(5)  

The time-invariance property of a transformation is, more precisely, a translation- invariance property that guarantees that a translation, by , of to has no effect on other than a corresponding translation to (exercise 1). A phenomenon is said to be time-invariant only if it is persistent in the sense that it is appropriate to conceive of a mathematical model of for which the following limit time-average exists for each value of and is not identically zero,³

(6)  

This function is called the limit autocorrelation function⁴ for . For , (6) is simply the time-averaged value of the instantaneous power.⁵

Sinewave analysis is especially appropriate for studying a convolution because the principal components (eigenfunctions) of the convolution operator are the complex sinewave functions, for all real values of . This follows from the facts that (1) the convolution operation produces a continuous linear combination of time-translates, that is, is a weighted sum (over ) of , and (2) the complex sinewave is the only bounded function whose form is invariant (except for a scale factor) to time-translation, that is, a bounded function satisfies

(7)  

for all if and only if

(8)  

for some complex and real (exercise 3). As a consequence, the form of a bounded function is invariant to all convolutions if and only if , in which case (5) yields

(9)  

for which

(10)  

This fact can be exploited in the study of convolution by decomposing a waveform into a continuous linear combination of sinewaves, ⁶

(11)  

with weighting function

(12)  

because then substitution of (11) into (5) yields

(13)  

for which

(14)  

Thus, any particular sinewave component in , say

(15)  

can be determined solely from the corresponding sinewave component in , since (14) and (15) yield

(16)  

The scale factor is the eigenvalue associated with the eigenfunction of the convolution operator. Transformations (11) and (12) are the Fourier transform and its inverse, abbreviated by

Statistical (time-averaged) analysis of waveforms into sinewave components is especially appropriate for time-invariant phenomena because an ideal statistical spectrum, in which all random effects have been averaged out, exists if and only if the limit autocorrelation (6) exists. Specifically, it is shown in Chapter 3 that the ideal statistical spectrum obtained from (3) by smoothing over all time,

exists if and only if the limit autocorrelation exists. Moreover, this ideal statistical spectrum can be characterized in terms of the Fourier transform of , denoted by

(17)  

Specifically,

(18)  

for which is the unit-area sinc-squared function with width parameter ,

(19)  

As the time-interval of spectral analysis is made large, we obtain (in the limit)

(20)  

because the limit of is the Dirac delta

(21)  

and convolution of a function with the Dirac delta as in (18) leaves the function unaltered (exercise 2). The ideal statistical spectrum defined by (20) is called the limit spectrum. It is worth emphasizing here that it is conceptually misleading to define the limit spectrum (also called the power spectral density) in terms of the limit autocorrelation using (17), as is unfortunately done in many text books. The meaning of the limit spectrum comes from (20), which is its appropriate definition. The equation (17) is simply a characterization of the limit spectrum.

Before leaving this topic of justifying the focus on sinewave components for time-series analysis, it is instructive (especially for the reader with a background in stochastic processes) to consider how the justification must be modified if we are interested in probabilistic (ensemble-averaged) statistical spectra rather than deterministic (time-averaged) statistical spectra. Let us therefore consider an ensemble of random samples of waveforms , indexed by ; for convenience in the ensuing heuristic argument, let us assume that the ensemble is a continuous ordered set for which the ensemble index, , can be any real number. For each member of the ensemble, we can obtain an analysis into principal components (sinewave components). A characteristic property of a set of principal components is that they are mutually uncorrelated ⁷ in the sense that

(22)  

where * denotes complex conjugation (exercise 5). But in the probabilistic theory, it is required that the principal components be uncorrelated over the ensemble⁸

(23)  

as well as uncorrelated over time in order to obtain the desired simplicity in the study of time-series subjected to LTI transformations. If we proceed formally by substitution of the principal component,

(24)  

into (23), we obtain⁹ (after reversing the order of the limit operation and the two integration operations)

(25)  

for which the function is the probabilistic autocorrelation defined by

(26)  

It can be shown (exercise 6) that (23) is valid if and only if

(27)  

for all translations , in which case depends on only the difference of its two arguments,

(28)  

Consequently principal-component methods of study of an LTI transformation of an ensemble of waveforms are applicable if and only if the correlation of the ensemble is translation invariant. Such an ensemble of random samples of waveforms is commonly said to have arisen from a wide-sense stationary stochastic process.¹⁰ But we must ask if ensembles with translation-invariant correlations are of interest in practice. As a matter of fact, they are for precisely the same reason that translation-invariant linear transformations are of practical interest. The reason is a preoccupation with time-invariance. That is, the ensemble of waveforms generated by some phenomenon will exhibit a translation-invariant correlation if and only if the data-generating mechanism of the phenomenon exhibits appropriate time-invariance. Such time-invariance typically results from a stable system being in a steady-state mode of operation—a statistical equilibrium. The ultimate in time-invariance of a data-generating mechanism is characterized by a translation-invariant ensemble, which is an ensemble for which the identity

(29)  

holds for all and all real ; that is, each translation by, for instance, of each ensemble member, such as , yields another ensemble member, for example, . This time-invariance property (29) is more than sufficient for the desired time-invariance property (27). An ensemble that exhibits property (29) shall be said to have arisen from a strict-sense stationary stochastic process. For many applications, a natural way in which a translation-invariant ensemble would arise as a mathematical model is if the ensemble actually generated by the physical phenomenon is artificially supplemented with all translated versions of the members of the actual ensemble. In many situations, the most intuitively pleasing actual ensemble consists of one and only one waveform, , which shall be called the ensemble generator. In this case, the supplemented ensemble is defined by

(30)  

The way in which a probabilistic model can, in principle, be derived from this ensemble is explained in Chapter 5, Section B. This most intuitively pleasing translation-invariant ensemble shall be said to have arisen from an ergodic¹¹ stationary stochastic process. Ergodicity is the property that guarantees equality between time-averages, such as (22), and ensemble-averages, such as (23). The ergodic relation (30) is known as Herman O. A. Wold’s isomorphism between an individual time-series and a stationary stochastic process [Wold 1948].

In summary, statistical sinewave analysis—spectral analysis as we shall call it—is especially appropriate in principle if we are interested in studying linear time-invariant transformations of data and data from time-invariant phenomena. Nevertheless, in practice, statistical spectral analysis can be used to advantage for slowly time-variant linear transformations and for data from slowly time-variant phenomena (as explained in Chapter 8) and in other special cases, such as periodic time-variation (as explained in Part II) and the study of the departure of transformations from linearity (as explained in Chapter 7).

Another Perspective

Basic science is built upon the analysis of data derived from observation, experimentation, and measurement (see Foreword). In the various fields of science, this data analysis often takes the form of spectral analysis for a variety of physical reasons. The following brief review of spectral terminology used throughout the sciences reveals how ubiquitous spectral analysis is in the sciences.

There are about 10 variations on the base word Spectrum, all relating to the same concept described above in this Section B—namely the set of strengths of the sinewave components into which a function of time can be decomposed via the procedure of spectral analysis. Here are the traditional definitions of all these various terms.

• Spectrum (noun); Spectra (plural); Spectro- (prefix relating to spectra); Spectral (adjective) –the following is adapted from https://en.wikipedia.org/wiki/Spectrum:

In the 17th century, the word spectrum was introduced into optics by Isaac Newton, referring to the range of colors observed when white light is dispersed through a prism. Before long, the term was adopted to referred to a plot of light intensity or power as a function of frequency or wavelength, also known as a spectral density plot.

The uses of the term spectrum expanded to apply to other waves, such as sound waves that could also be measured as a function of frequency, and the additional terms frequency spectrum and power spectrum of a signal were adopted. The spectrum concept now applies to any signal that can be measured or decomposed along a continuous variable such as energy in electron spectroscopy or mass-to-charge ratio in mass spectrometry.

The absorption spectrum of a chemical element or chemical compound is the spectrum of frequencies or wavelengths of incident radiation that are absorbed by the compound due to electron transitions from a lower to a higher energy state. The emission spectrum refers to the spectrum of radiation emitted by the compound due to electron transitions from a higher to a lower energy state. (The energy of radiation is proportional to the sinewave frequency of radiation; the proportionality factor is Planck’s constant.)

In astronomical spectroscopy, the strength, shape, and position of absorption and emission lines, as well as the overall spectral energy distribution of the continuum, reveal many properties of astronomical objects. Stellar classification is the categorization of stars based on their characteristic electromagnetic spectra. The spectral flux density is used to represent the spectrum of a light-source, such as a star.

In physics, the energy spectrum (not to be confused with energy spectral density) of a particle is the number of particles or intensity of a particle beam as a function of particle energy. Examples of techniques that produce an energy spectrum are alpha-particle spectroscopy, electron energy loss spectroscopy, and mass-analyzed ion-kinetic-energy spectrometry.

In mathematics, the spectrum of a matrix is the finite ordered set of eigenvalues of the matrix. (A matrix is a linear transformation of one vector—a finite ordered set of numerical values—into another vector.) In functional analysis, the spectrum of an operator is the countable set of eigenvalues of the (bounded) operator. (An operator is a linear transformation of one function-space vector—an ordered continuum of numerical values called a real-valued function of a real variable—into another function-space vector.) The eigenvectors of a linear time-invariant operator (a convolution) are the set of sinusoidal functions corresponding to all frequencies which comprise the entire set of real numbers. Therefore, the eigenvalues determine the amount the spectral components of a function are scaled when the function is transformed by a convolution. Hence, the use of the term spectrum for the set of eigenvalues. The spectrum of the convolution multiplies the spectrum of the function being convolved to produce the spectrum of the resultant convolved function.

• Spectrogram/Spectrograph/Spectrometer

A spectrogram, produced by an apparatus referred to as a spectrograph or spectrometer, especially in acoustics, is a visual representation of the frequency spectrum of, for example, sound as a function of time or another variable.

• Spectroscopy/Spectrometry

A spectrometer is a device used to record spectra and spectroscopy is the use of a spectrometer for chemical analysis.

===============

² Readers in need of a brief remedial review of the prerequisite topic of linear time-invariant transformations and the Fourier transform should consult Appendix I at the end of Chapter 1.

³ In Part II, it is explained that periodic and almost periodic phenomena as well as constant (time-invariant) phenomena satisfy (6). For to be from a constant phenomenon, it must satisfy not only (6) but also for all .

⁴ In some treatments of time-series analysis (see [Jenkins and Watts 1968]), the function (6) modified by subtraction of the mean

from , is called the autocovariance function, and when normalized by it is called the autocorrelation function.

⁵ If is the voltage (in volts) across a one-ohm resistance, then is the power dissipation (in Watts).

⁶ If is absolutely integrable, then (11) and (12) are the usual Fourier transform pair, but if is a persistent waveform (which does not die out as ) from a time-invariant phenomenon, then (11) and (12) must be replaced with the generalized (integrated) Fourier transform [Wiener 1930], in which case (14) becomes the Stieltjes integral [Gardner 1985]. The sine wave in (15) and (16) must be multiplied by to represent the infinitesimal sinewave components contained in and .

⁷ For a persistent waveform (which does not die out as ) from a time-invariant phenomenon, the property of sinewave components being mutually uncorrelated is deeper than suggested by (22). In particular, the envelopes (from (1)), and , of the local sinewave components (cf. Chapter 4, Section E) become uncorrelated in the limit for all as explained in Chapter 7, Section C.

⁸ The limit averaging operation in (23) can be interpreted (via the law of large numbers) as the probabilistic expectation operation.

⁹ To make the formal manipulation used to obtain (25) rigorous, must be replaced with the envelope of the local sinewave component, which is obtained from (1) with replaced by ; then the limit, , must be taken. An in-depth treatment of this topic of spectral correlation is introduced in Chapter 7, Section C, and is the major focus of Part II.

¹⁰ The term stochastic comes from the Greek to aim (guess) at.

¹¹ The term ergodic comes from the Greek for work path, which—in the originating field of statistical mechanics—relates to the path, in one dimension, described by , of an energetic particle in a gas.

C. ORIGINS OF SPECTRAL ANALYSIS

The Fourier theory of sine wave analysis of functions has its origins in two fields of investigation into the nature of the physical world: acoustical/optical wave phenomena and astronomical and geophysical periodicities.¹² These two fields have furnished the primary stimuli from the natural sciences to the classical study—which extends into the first half of the twentieth century—of spectral analysis. The motions of the planets, the tides, and irregular recurrences of weather, with their hidden periodicities and disturbed harmonics, form a counterpart of the vibrating string in acoustics and the phenomena of light in optics. Although the concept of sine wave analysis has very early origins, the first bona fide uses of sine wave analysis apparently did not occur until the eighteenth century, with the work of Leonhard Euler (1707—1783) and Joseph Louis Lagrange (1736—1813) in astronomy [Lagrange l772].¹³

The concept of statistical spectral analysis germinated in early studies of light, beginning with Isaac Newton’s prism experiment in 1664 which led to the notion that white light is simply an additive combination of homogeneous monochromatic vibrations. The developing wave optics ideas, together with developing ideas from meteorology and astronomy, led Sir Arthur Schuster (1851—1934), around the turn of the nineteenth century, to the invention of the periodogram for application to the problem of detecting hidden periodicities in random data [Schuster 1894, 1897, 1898, 1900. 1904. 1906, 1911]. The periodogram, denoted by (originally defined for discrete-time data), is simply the squared magnitude of the Fourier transform of a finite segment of data, , normalized by the length, , of the data segment (graphed versus the frequency variable, ):

(31)  

(32)  

where is taken to be zero for . if a substantial peak occurred in the periodogram, it was believed that an underlying periodicity of the frequency at which the peak occurred had been detected. As a matter of fact, this idea preceded Schuster in the work of George Gabriel Stokes (1819—1903) [Stokes 1879]; and a related approach to periodicity detection developed for meteorology by Christoph Hendrik Diederik Buys-Ballot (1817—1890) preceded Stokes [Buys- Ballot 1847]. The first general development of the periodogram is attributed to Evgency Evgenievich Slutsky (1880—1948) [Slutsky 1929, 1934].

Another approach to detection of periodicities that was being used in meteorology in the early part of the twentieth century was based on the correlogram [Clayton 1917; Alter 1927; Taylor 1920, 1938], whose earliest known use [Hooker 1901] was motivated by the studies in economics of John Henry Poynting (1852— 1914) [Poynting 1884]. The correlogram, denoted by (originally defined for discrete-time data), is simply the time-average of products of time-shifted versions of a finite segment of data (graphed versus the time-difference variable,),

(33)  

But since is zero for outside , we obtain

(34)  

If an oscillation with occurred in the correlogram, it was believed that an underlying periodicity had been detected.¹⁴

The discovery of the periodogram-correlogram relation (e.g., [Stumpff 1927; Wiener 1930]) revealed that these two methods for periodicity detection were, in essence, the same. The relation, which is a direct consequence of the convolution theorem (Appendix 1-1 at the end of Chapter 1) is that and are a Fourier transform pair (exercise 10):

This relation was apparently understood and used by some before the turn of the century, as evidenced by the spectroscopy work of Albert Abraham Michelson (1852—1931), who in 1891 used a mechanical harmonic analyzer to compute the Fourier transform of a type of correlogram obtained from an interferometer for the purpose of examining the fine structure of the spectral lines of lightwaves.

A completely random time-series is defined to be one for which the discrete-time correlogram is asymptotically () zero for all nonzero time-shifts, , indicating there is no correlation in the time-series. A segment of a simulated completely random time-series is shown in Figure 1-1(a), and its periodogram and correlogram are shown in Figures 1-1(b) and 1-1(c). This concept arose (originally for discrete-time data) around the turn of the century [Goutereau 1906]. and a systematic theory of such completely random time-series was developed in the second decade by George Udny Yule (1871—1951) [Yule 1926]. Yule apparently first discovered the fact that an LTI transformation (a convolution) can introduce correlation into a completely random time series. It is suggested by the periodogram-correlogram relation that a completely random time series has a flat periodogram (asymptotically). By analogy with the idea of white light containing equal amounts of all spectral components (in the optical band), a completely random time series came to be called white noise. As a consequence of the discoveries of the correlation-inducing effect of an LTI transformation, and the periodogram-correlogram relation, it was discovered that a completely random time series, subjected to a narrow-band LTI transformation, can exhibit a periodogram with sharp dominant peaks, when in fact there is no underlying periodicity in the data. This is illustrated in Figure 1-2. This revelation, together with several decades of experience with the erratic and unreliable behavior of periodograms, first established as an inherent property by Slutsky [Slutsky 1927], led during the mid—twentieth century to the development of various averaging or smoothing (statistical) methods for modifying the periodogram to improve its utility. A smoothed version of the periodogram in Figure 1-1(b) is shown in Figure 1-1(d). Such averaging techniques were apparently first proposed by Albert Einstein (1879—1955) [Einstein 1914], Norbert Wiener(1894—1964) [Wiener 19301 and later by Percy John Daniell (1889—1946) [Daniell 1946], Maurice Stevenson Bartlett (1910—) [Bartlett 1948, 1950], John Wilder Tukey (1915—) [Tukey 1949], Richard Wesley Hamming (1915—), and Ralph Beebe Blackman (1904—) [Blackman and Tukey 1958]. In addition, these circumstances surrounding the periodogram led to the alternative time-series-modeling approach to spectral analysis, which includes various methods such as the autoregressive-modeling method introduced by Yule [Yule 1927] and developed by Herman O. A. Wold (1908—) [Wold 1938] and others.

Apparently independent of and prior to the introduction (by others) of empirical averaging techniques to obtain less random measurements of spectral content of random time-

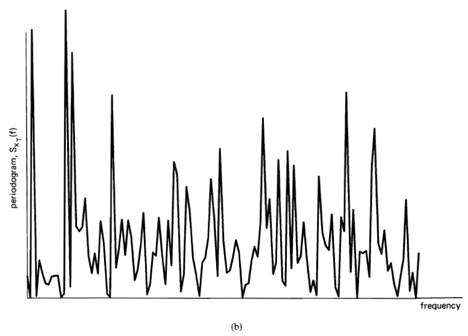
Figure 1-1 (a) Completely random data (white noise), . (b) Periodogram of white noise, .

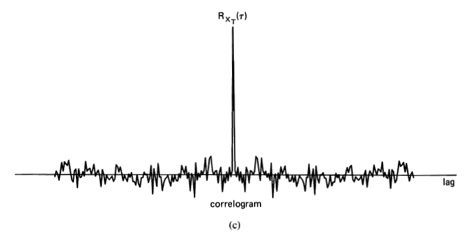
Figure 1-1 (continued) (c) Corrrelogram of white noise, . (d) Smoothed periodogram of white noise, , .

series, Wiener developed his theory of generalized harmonic analysis [Wiener 1930], in which he introduced a completely nonrandom measure of spectral content. Wiener’s spectrum can be characterized as a limiting form of an averaged periodogram. In terms of this limiting form of periodogram and the corresponding limiting form of correlogram, Wiener developed what might be called a calculus of averages for LTI transformations of time-series. Although it is not well known, ¹⁵ Wiener’s limit spectrum and its characterization as the Fourier transform of a limit

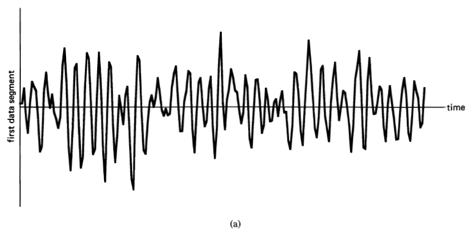
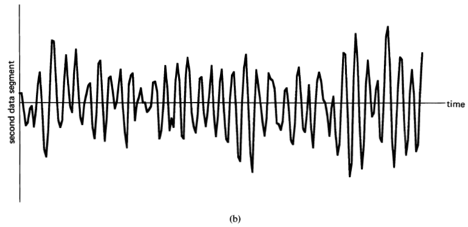
Figure 1-2 (a), (b) Two segments of narrow-band data, .

correlogram had been previously presented (in rather terse form) by Einstein [Einstein 1914].

The autonomous development of statistical mechanics, with Josiah Willard Gibbs’ (1839—1903) concept of an ensemble average, and the study of Brownian motion, by Maryan von Smoluchowski [von Smoluchski 1914], Einstein [Einstein 1906], and Wiener [Wiener 1923], together with the mathematical development of probability theory based on the measure and integration theory of Henri León Lebesgue (1875—1941) around the turn of the century, led ultimately to the probabilistic theory of stochastic processes. This theory includes a probabilistic counterpart to Wiener’s theory of generalized harmonic analysis, in which infinite time-averages are replaced with infinite ensemble averages. It greatly enhanced the conceptualization and mathematical modeling of erratic-data sources and the design and analysis of statistical data-processing techniques such as spectral analysis. The theory (for discrete-time processes) originated in the work of Aleksandr Jakovlevich Khinchin (1894—1959) during the early 1930s [Khinchin 1934] and was further developed in the early stages by Wold [Wold 1938], Andrei Nikolaevich Kolmogorov (1903—) [Kolmogorov 1941a,b], and Harald Cramér (1893—) [Cramér 1940, 1942].¹⁶ Major contributions to the early development of the probabilistic theory and methodology of statistical spectral analysis were made by Ulf Grenander and Murray Rosenblatt [Grenander and Rosenblatt 1953, 1984], Emanuel Parzen [1957a, b], and Blackman and Tukey [Blackman and Tukey 1958].

The probabilistic theory of stochastic processes is currently the popular approach to time-series analysis. However, from time to time, the alternative deterministic approach, which is taken in this book, is promoted for its closer ties with empirical reality for many applications; see [Kampé de Fériet 1954; Brennan 1961; Bass 1962; Hofstetter 1964; Finch 1969; Brillinger 1975, Sec. 2.11; Masani 1979].

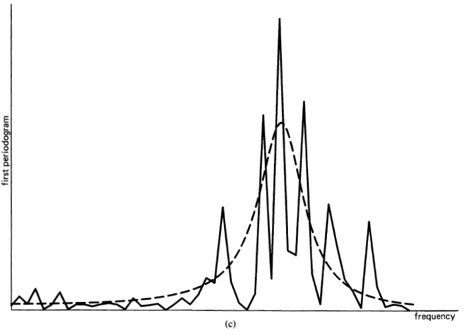
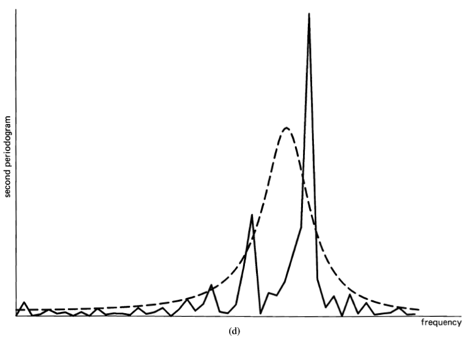
Figure 1-2 (continued) (c), (d) Periodograms of the two data segments shown in (a) and (b). (Broken curve is the limit spectrum.)

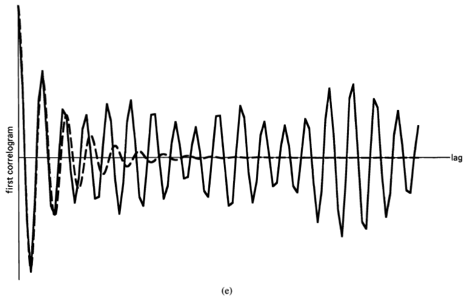
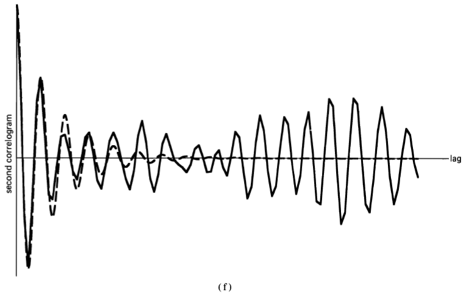
Figure 1-2 (continued) (e), (f) Correlograms of the two data segments shown in (a) and (b). (Broken curve is the limit autocorrelation.)
===============

¹³ See [Wiener 1938; Davis 1941; Robinson 1982] for the early history of spectral analysis. and [Chapman and Bartels 1940, Chapter XVI] for an account of early methods.

¹⁴The early history of correlation studies is reported in [Davis 1941].

¹⁵This little-known fact was brought to the author’s attention by Professor Thomas Kailath, who learned of it from Akiva Moisevich Yaglom.

¹⁶The most extensive bibliography on time-series and random processes, ranging from the earliest period of contribution (mid-nineteenth century) to the recent past (1960) is the international team project bibliography edited by Wold [Wold 1965]. Starting with 1960, a running bibliography, including abstracts, is available in the Journal of Abstracts:Statistical Theory and Method.

E. SUMMARY

Section A explains that the objective of Part I of this book is to show that a comprehensive deterministic theory of statistical spectral analysis, which for many applications relates more directly to empirical reality than does its more popular probabilistic counterpart, can be (and is in this book) developed—the motivation being to stimulate a reassessment of the way engineers and scientists are often taught to think about statistical spectral analysis by showing that probability theory need not play a primary role. In Section B it is explained that the most basic purpose of spectral analysis is to represent a function by a sum of weighted sinusoidal functions called spectral components and that procedures for statistical spectral analysis average the strengths of such components to reduce random effects. It is further explained that sine wave components, in comparison with other possible types of components, are especially appropriate for analyzing data from time invariant phenomena, because sine waves are the principal components of time invariant linear transformations and because an ideal sine wave spectrum exists if and only if the data source is time-invariant (in an appropriate sense specified herein). The conceptual link between this practical empirically-motivated point of view and that of the more abstract probabilistic framework of ergodic stationary stochastic processes on which statistical spectral analysis is typically based is then explained in terms of Wold’s isomorphism. In Section C, a historical sketch of the origins of spectral analysis is presented, and finally in Section D the need for a generalization of the theory of spectral analysis of random data, from constant phenomena to periodic phenomena, is commented upon.

Appendix 1-1 is a brief review of prerequisite material on linear time-invariant transformations and the Fourier transform.

F. OVERVIEW OF PART I

This first chapter is concluded with a brief overview of the remainder of Part I. In Chapter 2, the basic elements of empirical spectral analysis are introduced. The time-variant periodogram for nonstatistical spectral analysis is defined and characterized as the Fourier transform of the time-variant correlogram, and its temporal and spectral resolution properties are derived. The effects of linear time-invariant filtering and periodic time sampling are described. Then in Chapter 3, the fundamentals of statistical spectral analysis are introduced. The equivalence between statistical spectra obtained from temporal smoothing and statistical spectra obtained from spectral smoothing is established, and the relationship between these statistical spectra and the abstract limit spectrum is derived. The limit spectrum is characterized as the Fourier transform of the limit autocorrelation, and the effects of linear time-invariant filtering and periodic time-sampling on the limit spectrum are described. Various continuous-time and discrete-time models for time-series are introduced, and their limit spectra are calculated. Chapter 4 presents a wide variety of analog (continuous-time) methods for empirical statistical spectral analysis, and it is shown that all these methods are either exactly or—when a substantial amount of smoothing is done—approximately equivalent. The spectral leakage phenomenon is explained, and the concept of an effective spectral smoothing window is introduced. Then a general representation for the wide variety of statistical spectra obtained from these methods is—possibly for the first time—introduced and shown to provide a means for a unified study of statistical spectral analysis. In Chapter 5, it is explained that the notion of the degree of randomness or variability of a statistical spectrum can be quantified in terms of time-averages by exploiting the concept of fraction-of-time probability. This approach is then used mathematically to characterize the temporal bias and temporal variability of statistical spectra. These characterizations form the basis for an in-depth discussion of design trade-offs involving the resolution, leakage, and reliability properties of a statistical spectrum. The general representation introduced in Chapter 4 is used here to obtain—possibly for the first time—a unified treatment of resolution, leakage, and reliability for the wide variety of spectral analysis methods described in Chapter 4. Chapter 6 complements Chapter 4 by presenting a variety of digital (discrete-time) methods for statistical spectral analysis. Chapter 7 generalizes the concept of spectral analysis of a single real-valued time-series to that of cross-spectral analysis of two or more complex-valued time-series. It is established that the cross spectrum, which is a measure of spectral correlation, plays a fundamental role in characterizing the degree to which two or more time-series are related by a linear time-invariant transformation. Methods for measurement of statistical cross spectra that are generalizations of the methods described in earlier chapters are presented, and the temporal bias and temporal variability of statistical cross spectra are mathematically characterized—possibly for the first time—in a unified way based on a general representation. In Chapter 8, the application of statistical spectral analysis to time-variant phenomena is studied. Fundamental limitations on temporal and spectral resolution are discussed, and the roles of ensemble averaging and probabilistic models are described. Finally, in Chapter 9, an introduction to the theory of autoregressive modeling of time-series is presented and used as the basis for describing in an unified manner a variety of autoregressive parametric methods of statistical spectral analysis. In keeping with the theme of this book, the unification is carried out within the time-average framework, thereby avoiding the unnecessary abstraction of stochastic processes. The chapter concludes with an extensive experimental study and comparison of various parametric and nonparametric methods of statistical spectral analysis.

Chapter 2, NONSTATISTICAL SPECTRAL ANALYSIS

I. SUMMARY

In Section A, the time-variant periodogram, which is the squared magnitude of the time-variant finite-time complex spectrum normalized by the data-segment length , is introduced as an appropriate measure of local spectral content of a waveform; it is established that the temporal resolution width of the time-variant periodogram is , and the spectral resolution width is on the order of . In Section B, the technique of data tapering is introduced as a means for controlling the shape of the effective spectral smoothing window in the periodogram, and several basic tapering apertures or windows are introduced. Then Section C explains that regardless of the particular tapering aperture used, the product of temporal and spectral resolution widths is always on the order of unity, because the corresponding temporal and spectral windows are a Fourier transform pair. In Section D, the time-variant correlogram is introduced as a measure of local autocorrelation of a waveform, and it is established that the time-variant periodogram is the Fourier transform of the time-variant correlogram. Then in Section E, an alternative measure of local autocorrelation termed the finite-average autocorrelation is introduced, and its Fourier transform, the pseudospectrum, is claimed to be a useful alternative to the periodogram when it is appropriately averaged to obtain a statistical spectrum. Several exact and approximate relationships among time-averaged correlograms and time-averaged finite-average autocorrelations are established for their use in the next chapter, where time-averaged measures of spectral content are studied. It is also explained that in the limit as the parameter approaches infinity both the correlogram and finite-average autocorrelation approach the ideal limit autocorrelation. In Section F, an approximate convolution relation between the correlograms (and finite-average autocorrelations) at the input and output of a filter is derived and then used to derive an approximate product relation between the corresponding periodograms (and pseudospectra). It is explained that these approximate relations become exact in the limit as the parameters in (35) and (37) and in (39) and (40) approach infinity. These are referred to as the (input/output) limit-autocorrelation relation and limit-spectrum relation for filters, (38) and (41). In Section G, the approximate periodogram relation for filters is used to establish that the time-variant periodogram can be interpreted as a measure of local-average power spectral density only if the temporal and spectral resolutions are limited in order to satisfy the time- frequency uncertainty condition (51). Finally in Section H, the discrete-time counterpart of the continuous-time complex spectrum is introduced, and the spectral aliasing phenomenon associated with time-sampling is described. Then the discrete-time counterparts of the time-variant periodogram and time-variant correlogram are introduced, and it is established that these are a Fourier-series transform pair.

In Appendix 2-1 at the end of Chapter 2, the concept of instantaneous frequency for a sine wave with a time-variant argument is introduced and used to illustrate the resolution limitations of the time-variant periodogram.

For the sake of emphasis, two basic and fundamental results on the relationships between the overall widths and the resolution widths of Fourier transform pairs that are developed in this chapter and the exercises are repeated here at the conclusion of this summary. If a time-function has overall width (duration) on the order of , then the spectral resolution width of its transform must be on the order of . Furthermore, if the time-function is pulselike, then its temporal resolution width is on the order of its overall width . Similarly, if a frequency function has overall width (bandwidth) on the order of , then the temporal resolution width of its inverse transform must be on the order of , and if the frequency function is pulselike (low-pass or band-pass) then its spectral resolution width is on the order of its overall width . These simple order-of-magnitude rules are a key to understanding the principles of spectral analysis resolution.

Chapter 3, STATISTICAL SPECTRAL ANALYSIS

This chapter introduces the fundamentals of statistical spectral analysis: the equivalence between statistical spectra obtained from temporal smoothing and statistical spectra obtained from spectral smoothing, and the relationship between these statistical spectra and the abstract limit spectrum. The motivation for smoothing—to average out undesired random effects that mask spectral features of interest—is developed by consideration of the problem of measuring the parameters of a resonance phenomenon. It is established that the limit autocorrelation and limit spectrum are a Fourier transform pair and that each is a self-determinate characteristic under a linear time-invariant transformation (filtering operation). The utility of the limit spectrum for characterizing spectral features in stationary time-series is illustrated with several examples of modulated waveforms. Periodically time-sampled waveforms are considered, and a formula for the limit spectrum of the discrete-time sampled data, in terms of the limit spectrum of the waveform, is derived and used to describe further the spectral aliasing phenomenon. The moving average and autoregressive models of discrete-time data are introduced, and their limit spectra are derived. In Appendix 3-1 at the end of Chapter 3, bandpass time-series are considered and a general representation in terms of lowpass time-series is derived, and the relationships between the limit autocorrelations and limit spectra of the bandpass and lowpass time-series also are derived. In Appendix 3-2, the role of spectral analysis in the detection of random signals is explained.

A. MOTIVATING EXAMPLE

In order to understand why a statistical (average) spectrum can be preferable to a nonstatistical spectrum, we must focus our attention not on the data itself but rather on the source of the data—the mechanism that generates the data. Generally speaking, data is nothing more than a partial representation of some phenomenon—a numerical representation of some aspects of a phenomenon. The fundamental reason for interest in a statistical (e.g.. time-averaged) spectrum of some given data is a belief that interesting aspects of the phenomenon being investigated have spectral influences on the data that are masked by uninteresting (for the purpose at hand) random effects and an additional belief (or, at least, hope) that these spectral influences can be revealed by averaging out the random effects. This second belief (or hope) should be based on the knowledge (or, at least, suspicion) that the spectral influences of the interesting aspects of the phenomenon are time-invariant, so that the corresponding invariant spectral features (such as peaks or valleys) will be revealed rather than destroyed by time-averaging.

This idea is illustrated with the following example. Consider the problem of determining the resonance frequency and damping ratio of a single-degree-of-freedom mechanical system (see exercise 10) that is subject to a continuous random vibrational force excitation . The system displacement response can be modeled as an LTI transformation of the excitation, with the transfer function magnitude shown in Figure 3-1, which reveals the resonance frequency and the bandwidth (which can be related to the damping ratio). The vibrational response of the system is random by virtue of the randomness of the excitation. Consequently, the spectrum of the response data does not exhibit the desired single smooth peak shown in Figure 3-1. Rather, it is an erratic function with numerous sharp peaks and valleys, as revealed by the simulation shown in Figure 3-2(a). Moreover, as the time-interval of analysis is made longer by increasing , the spectrum only becomes more erratic (at least locally), as revealed by the simulation shown in Figure 3-2(b). However, if the random excitation arises from a system in statistical equilibrium, the underlying time-invariance in the excitation, as well as in the resonant system, suggests that time-averaging the response spectrum will reduce the random effects while leaving the desired spectral features intact. In fact, it is shown in the next section that for , the time-smoothed spectrum,

(1)  

is closely approximated by the frequency-smoothed spectrum

(2)  

and for sufficiently large and the particular form of the spectral-smoothing window is irrelevant. Consequently, approximation (40) in Chapter 2 can be used to obtain

(3)  

for which it has been assumed that¹

(4)  

where is the resolution width of the function ( is on the order of , where is the system memory length—the width of ). If the system excitation is completely random so that it exhibits no spectral features, then for , will closely approximate a constant (over the support for which is nonnegligible), say . Therefore, (3) yields the desired result:

(5)  

from which the resonance frequency and damping ratio can be determined. This is illustrated with the simulations shown in Figure 3-2 (c) and (d).

In addition to illustrating the use of a statistical spectrum obtained from time-smoothing a periodogram (1), this example introduces the idea that an equivalent statistical spectrum can also be obtained from frequency-smoothing a periodogram (2). This equivalence is established in the following section. However, before proceeding it should be clarified that in practice when automated spectrum analyzers are used to study visually the spectral features of a phenomenon, it is common practice to use very little smoothing (and in some cases no smoothing) in spite of the erratic behavior of the displayed spectrum due to random effects. But it should be remembered that human visual perception incorporates spatial integration and temporal memory so that we in effect perceive a smoothed spectrum even when the analyzer uses no smoothing. This is apparent from Figure 3-2 (a) and (b), in which we can perceive the smoothed spectra that are shown in Figure 3-2 (c) and (d).

Figure 3-1 Magnitude-squared transfer function of resonant system.

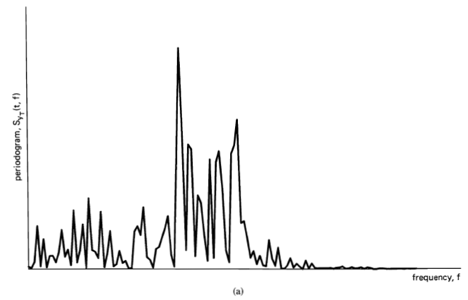
Figure 3-2 Nonstatistical spectra of response of resonant system to completely random excitation. (Length of time interval of analysis is ): (a) , (b) .

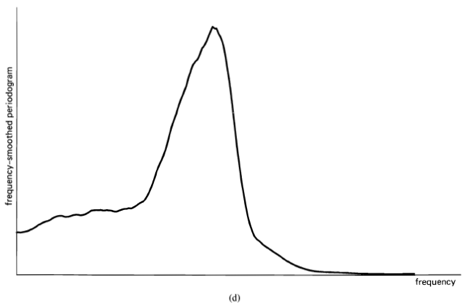
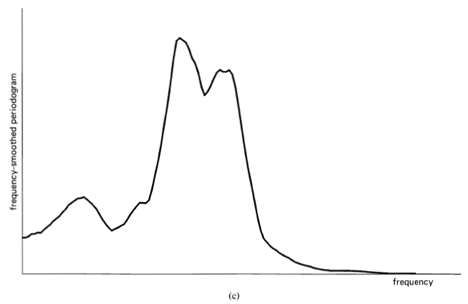
Figure 3-2 (continued) Statistical spectra obtained by frequency-smoothing the nonstatistical spectra shown in (a) and (b): (c) from (a) with , (d) from (b) with .
===============

¹Condition (4) guarantees that the order of multiplication with and convolution with in(40), Chapter 2, can be interchanged to obtain a close approximation.

G. STATISTICAL INFERENCE

In the spectral analysis problem considered in Section A, the spectral features of interest as described by can be measured only approximately with a finite amount, , of data, as indicated by approximation (5). But as shown in subsequent sections, can be determined exactly in the abstract limit as , as indicated by (28) and (38). This reveals that exact description of the spectral characteristics of a phenomenon requires an abstract mathematical model for the data, namely, the limit spectrum.

We have thus arrived at the point of view of statistical inference, which is that an abstract mathematical model is the desired result that can be only approximately discovered (inferred) with the use of a finite amount of data.

From the point of view of statistical inference, the object of statistical spectral analysis is spectrum estimation, by which is meant estimation of the limit spectrum.¹³ Succinctly stated, the classical spectrum estimation design problem is: given a finite amount¹⁴ of data, determine the best value of spectral resolution to obtain the best estimate of . This involves a trade-off between maximizing spectral resolution, which corresponds to minimizing and minimizing the degree of randomness or variability (described in Chapter 5), which in turn corresponds to maximizing in order to maximize the product .

The statistical-inference or spectrum-estimation interpretation given here to spectral analysis is unconventional in that it does not rely on probabilistic concepts.

However, it can be put into a probabilistic framework by reinterpreting infinite time averages as ensemble averages (expectations) via H. O. A. Wold’s isomorphism (defined in Chapter 1, Section B). This is done in Chapter 5, where the notion of degree of randomness is quantified in terms of a coefficient of variation that is shown to be inversely proportional to the resolution product .

As a matter of fact, the classical spectrum estimation design problem is more involved than suggested by the preceding succinct statement, because the shape as well as the width of the effective spectral window should be optimized in order to minimize the undesirable spectral leakage effect. This effect is described in the next chapter, and the design problem that simultaneously takes into account resolution, leakage, and degree of randomness is explained in Chapters 5 and 6.

Before proceeding, a few words about the notion of degree of randomness will be helpful to tide us over until the subject is taken up in Chapter 5. It has been shown in this chapter that randomly fluctuating (in both and ) statistical spectra, such as and , converge in the limit (, ) to the nonrandom limit spectrum if the limit autocorrelation exists, which is necessary for a constant phenomenon. The degree of randomness or variability of a statistical spectrum can be interpreted as the degree to which the statistical spectrum varies from one point in time to another. If the underlying phenomenon is indeed constant, as hypothesized in Part I, then fluctuation with time of the statistical spectrum must be attributed to random effects. it is shown in Chapter 5 that the time-averaged squared difference between statistical spectra measured at two different times separated by an amount , for example, is approximately inversely proportional to the resolution product (for sufficiently small and sufficiently large ) for all . Also, the time-averaged squared difference between the statistical spectrum and the nonrandom limit spectrum behaves in the same way. Thus, this temporal mean-square measure of the degree of randomness of a statistical spectrum reveals that the degree of randomness is made low (or the reliability is made high) by making the resolution product large.

This central characteristic of statistical spectral analysis has been arrived at without resorting to the mathematical artifice of pretending the data is one member of an ensemble corresponding to a stochastic process, and then interpreting degree of randomness as variability over the make-believe ensemble—which is a huge departure from empirical reality.

This key result exposes the confusion that reigns in efforts to understand empirical data in terms of the unnecessary theory of stochastic processes.

Note dated June 2020: The several negative reviews of this book written within a few years of its publication in 1987 and at strong odds with the positive reviews clearly reveal this common state of confusion even among experts judged worthy of reviewing technical books. (See page 3.3 of this website.)
===============

¹³In the literature, the terms spectrum analysis and spectral estimation are often used in place of the terms spectral analysis and spectrum estimation, which are used in this book, the latter two terms are more appropriate since we are not concerned with analysis of a spectrum but rather with analysis of data into spectral components, and we are not concerned with estimation using spectral methods but rather with estimation of a spectrum. Nevertheless, because of the long-standing tradition of referring to spectral analysis instruments as spectrum analyzers, this term is used in this book in place of the term spectral analyzers.

¹⁴ The actual amount of data needed to average a periodogram of length over an interval of length is , but this is closely approximated by for .

H. SUMMARY

In Section A, the problem of measuring the parameters of a resonance phenomenon from the randomly resonant response to random excitation is considered in order to motivate consideration of averaging methods for reducing random effects. It is explained that from the point of view adopted here, we focus attention on the phenomenon that gives rise to random data rather than on the data itself, and we apply averaging methods to the nonstatistical spectrum (periodogram) of the data to obtain a statistical spectrum in which the random effects in the data that mask the spectral influences from the phenomenon are reduced. In Section B, a profound fundamental result establishing an equivalence between time-smoothed and frequency-smoothed periodograms is developed. This equivalence reveals that the periodogram of the data-tapering window in a temporally smoothed periodogram of the tapered data is an effective spectral smoothing window in an equivalent spectrally smoothed periodogram of the untapered data. Then in Section C, the idealized limiting form of the statistical spectrum with and (in this order) is shown to be simply the Fourier transform of the limit autocorrelation. This characterization of the limit spectrum, called the Wiener relation, is used to derive the limit-spectrum relation for filters (28), which in turn is used to establish the interpretation of the limit spectrum as a spectral density of time-averaged power.

In Section C, several signal and noise models are introduced, and their limit spectra are calculated. Then in Section D, the definition of the limit spectrum is adapted to discrete-time data by simply replacing the Fourier transform with the Fourier-series transform introduced in Section H of Chapter 2. A spectral aliasing formula relating the limit spectra of a waveform and its time-samples is derived. In Section F, three basic time-series models for discrete-time data are introduced. These are the MA, AR. and ARMA models. Formulas for the limit spectra for these models are derived in terms of the parameters of the models.

Finally in Section G, it is pointed out that the arguments presented in the beginning of this chapter have led us to the point of view of statistical inference. which is that an abstract mathematical model—the limit spectrum in this case— is the desired result that can be only approximately discovered (inferred) with the use of a finite amount of data. Thus statistical spectral analysis is typically called spectrum estimation. This section ends with a brief discussion of the dependence of the degree of randomness or variability of a statistical spectrum on the resolution product .

In Appendix 3-1 at the end of Chapter 3, Rice’s representation is derived. This provides a means for representing band-pass waveforms in terms of low-pass waveforms. Then the limit spectra for the low-pass representors are characterized in terms of the limit spectrum of the band-pass waveform, and vice versa. In Appendix 3-2, the problem of detecting the presence of a random signal in additive random noise is considered, and the central role played by the periodogram and the limit spectrum is revealed.

Chapter 4, ANALOG METHODS

In Chapter 3 it is established that a statistical spectrum can be obtained from a periodogram by either the temporal-smoothing method or the spectral-smoothing method and that these two methods yield approximately the same statistical spectrum when a substantial amount of smoothing is done (). In this chapter it is shown that a variety of alternative methods yield approximately or exactly the same statistical spectrum, but it is emphasized that differences can be quite important in practice. These alternatives include the methods of temporal or spectral smoothing of the pseudospectrum, hopped temporal smoothing of the periodogram and pseudospectrum, Fourier transformation of the tapered correlogram and finite-average autocorrelation, real and complex wave-analysis, real and complex demodulation, and swept-frequency-demodulation wave-analysis. The methods are referred to as analog methods because they process the continuous-time waveforms directly. The actual form of implementation of such methods can employ conventional resistive-capacitive-inductive passive electrical circuits, more modern active electrical circuits, microwave devices, various optical, acousto-optical, and electro-acoustical devices, or mechanical devices. The particular form of implementation depends on available technology, economic constraints, environmental constraints (e.g., temperature, mechanical vibration, humidity, and so on), and frequency ranges of interest. The upcoming Chapter 6 presents digital methods, so called because they process discrete-time data and because digital electrical forms of implementation (both hardware and software) are the primary means for discrete-time processing.

H. SUMMARY

In this chapter, an introductory comparative study of a variety of analog (continuous-timeand continuous-amplitude) methods of measurement of statistical spectra is conducted. In Section A, approximate equivalences among the four methods based on temporal and spectral smoothing of the penodogram and pseudospeetrum are derived, and in Section B it is established that the two spectral smoothing methods are each exactly equivalent to a method consisting of Fourier transformation of a tapered autocorrelation function. The resultant eight distinct methods for obtaining the four distinct (but approximately equivalent) statistical spectra are summarized in Figures 4-1 and 4-2 (see below). In Section C, the spectral leakage phenomenon that results from the sidelobes of the effective spectral smoothing window is explained, and the sine-wave-removal, tapering, and prewhitening approaches to reducing spectral leakage are described. Then Section D explains that temporal smoothing based on continuously sliding periodograms or pseudospectra can be modified to obtain hopped periodograms or pseudospectra, and an exact equivalence between a hopped time-averaged pseudospectrum and a spectrally smoothed pseudospectrum is derived. A similar but approximate equivalence for the hopped time-averaged penodogram is derived in exercises I and 2.

In Section E, an alternative method for implementing the temporally smoothed periodogram, which is based on filtering is introduced. Both real and complex implementations, called wave analyzers, are developed (Figure 4-4, see below). Then in Section F, another alternative implementation based on demodulation is derived. The real and complex implementations of the demodulation spectrum analyzer (Figure 4-6, see below) can be obtained directly from the corresponding implementations of the wave analyzer by using band-pass-to-low-pass transformations on the filters (Figure 4-8). It is then explained that an economical way to construct a spectrum analyzer that covers a broad range of frequencies is to use the demodulation method and sweep the frequency of the sine wave used for demodulation. It is also explained that it is often more practical to use swept-frequency demodulation to down-convert all frequencies to a fixed nonzero intermediate frequency and then use the wave-analysis method (Figure 4-7, see below). In addition, an alternative method of swept-frequency spectral analysis that incorporates time compression is described in exercise 14.

Finally in Section G, a general representation for all preceding types of spectrum analyzers (except the swept-frequency wave analyzer) is introduced, possibly for the first time, and it is explained that the two width parameters and of the kernel that prescribes the representation for a particular spectrum analyzer determine the temporal and spectral resolution widths of the statistical spectrum produced by the analyzer. A convenient separable approximation (75) to the kernel is introduced, and it is explained that the resultant approximate and exact general representations provide a unifying basis for the design and analysis of spectrum analyzers. This is demonstrated in the next chapter.

In Appendix 4-1 at the end of Chapter 4, an alternative wave-analysis method that is equivalent to a method based on Fourier transformation of a tapered autocorrelation is presented.

Chapter 5, FRACTION-OF-TIME PROBABILISTIC ANALYSIS

E. SUMMARY

In this chapter the concept of fraction-of-time probabilistic analysis is introduced and used to quantify the resolution, leakage, and reliability properties of statistical spectra. In Section A it is explained that probabilistic analysis can be carried out without relying on the abstract notion of a probability space and an associated ensemble of random samples by using the concept of fraction-of-time probability. Then in Section B, the general fraction-of-time probabilistic model is defined and the particularly important special case, the Gaussian model, is defined. In Section C, the two temporal probabilistic measures of performance called bias and variability are defined and characterized in terms of the temporal mean, temporal coefficient of variation, and temporal correlation coefficient. These temporal probabilistic parameters are evaluated for the complex spectrum, periodogram, and various statistical spectra specified by the general representation introduced in Chapter 4, Section G. A general formula (50) – (51)for the effective spectral smoothing window is obtained and evaluated for various specific types of statistical spectra. A general formula (72) – (73) for the coefficient of variation is obtained, and it is simplified ((74) – (77)) by using the separable approximation to the kernel in the general representation (48), and the variability phenomenon is explained. Then two examples that illustrate the effects of variability are presented, and a time-frequency uncertainty principle for statistical spectra is described. Finally, the utility of the explicit formula for the effective spectral smoothing window is brought to light by explaining how it can be used in design to trade off resolution, leakage, and reliability performance (see Table 5-2). Two examples are presented to illustrate these design trade-offs. For situations in which the amount of data available is severely restricted or the range of the spectrum is large, such that the conditions required for the approximate formula for the coefficient of variation to be accurate are violated, the exact formulas for the mean (50) – (51) and variance (66) can be used simply by substituting in the kernel that specifies the particular spectrum estimate of interest (see Table 5-1). This is important because leakage effects that do not show up in the effective spectral smoothing window can be revealed in the variability when the exact formulas are used.

Chapter 6, DIGITAL METHODS

A. INTRODUCTION

Modern general-purpose spectral analysis instruments are typically implemented using primarily analog technology for frequencies above 100 KHz and digital technology for frequencies below 100 Hz, and both technologies are used in the midrange. The swept-frequency method described in Chapter 4 is the most commonly used analog method for general-purpose instruments, whereas the fast Fourier transform (FFT), with the discrete-time and discrete-frequency counterparts of the frequency smoothing and/or hopped time-averaging methods described in Chapter 4, is used for most digital implementations. Digital methods are especially attractive for low frequencies because the most attractive analog method (swept frequency) requires long measurement times compared with the simultaneous analysis methods based on Fourier transformation of the data. Analog methods are especially appropriate for high frequencies because of technological limitations on switching times, which limit the speed of digital computation. When the required speed is not a limiting factor, digital implementations are generally attractive because of economy as well as high accuracy, stability, and flexibility, including programmability. Furthermore, spectral analysis at frequencies far above 100 KHz can be accomplished digitally by down-converting spectral bands (of width less than 100 KHz) from higher frequency ranges (e.g., megahertz to gigahertz) to lower frequency ranges (below 100 KHz), and this band-selective approach can be used to obtain very high spectral resolution. Moreover, the flexibility of digital methods is an attractive feature for many special-purpose spectral analysis tasks, where general-purpose instruments are inappropriate. An example of this flexibility is the fact that digital methods can be directly implemented in software so that both the convenience of personal computers and the immense data-handling capabilities of supercomputers are available for spectral analysis. Finally, because of the increasing amount of data that is digitally encoded for storage and transmission, digital methods of spectral analysis that can be directly applied to digital data are especially appropriate.

Unfortunately, the study of digital methods of spectral analysis is somewhat more complicated than the study of analog methods for several reasons. These include 1) the spectral aliasing phenomenon that results from time-sampling. 2) the discrete nature of the frequency parameter in FFT and other discrete Fourier transform (DFT) algorithms, and 3) the block format for data that is required by DFT algorithms. All three of these items are sources of conceptual complication that can lead to complications in practice, including erroneous procedures and misinterpretation of results. Fortunately, many of the fundamentals of spectral analysis can be understood, as explained in the other chapters of this book, without introducing the complications associated with digital methods of implementation. This applies especially to the digital methods of spectral analysis that are simply discrete-time and discrete-frequency counterparts of the analog methods studied in Chapter 4.

In Section B, the DFT is introduced and its properties and relationships with other Fourier transformations are studied. Then in Section C, various digital counterparts of the analog methods developed in Chapter 4 are described. Finally in Section D, the applicability to discrete-time spectrum estimates of the results on fraction-of-time probabilistic analysis obtained in Chapter 5 for continuous time is explained.

E. SUMMARY

In Section A, the complementary nature of analog and digital methods of spectral analysis are discussed. Then in Section B the DFT, on which most digital methods are based, is studied. Topics include the use of zero-padding to control resolution, the distinction between circular and linear convolutions, the circular convolution theorem and the associated wraparound phenomenon, and a circular correlogram-periodogram relation. Also, the relationships among the DFT, FST, and CFT are described, and the importance of zero-padding is discussed and illustrated by example. In Section C various digital methods for statistical spectral analysis that are based on the DFT are described and compared. It is explained that these methods, known by the names Bartlett-Welch, Wiener-Daniell, Blackman-Tukey, and channelizer methods, are all digital counterparts of analog methods studied in Chapter 4. Then the minimum-leakage method, which is an optimized wave analyzer (channelizer), is derived and its interpretation in terms of maximum likelihood is explained. Finally in Section D, it is explained that the formulas derived in Chapter 5 for the mean and variance of continuous-time spectrum estimates apply equally well to discrete-time spectrum estimates, provided only that the range of integration over frequency variables is reduced from to [˗½, ½], to reflect the replacement of the CFT by the FST in the derivation.

Chapter 7, CROSS-SPECTRAL ANALYSIS

In this chapter, the concept of the spectral density of a single real-valued time-series is generalized to the concept of the cross-spectral density of two complex-valued time-series. Complex-valued time-series are considered in order to accommodate complex low-pass representations of real band-pass time-series (see Appendix 3-1). It is established that the cross spectrum, which is a measure of spectral correlation, plays a fundamental role in characterizing the degree to which two time-series are related by a linear time-invariant transformation. Methods for measurement of statistical cross spectra that are straightforward generalizations of the methods described in Chapter 4 for measurement of statistical spectra are described. The chapter concludes with a discussion of the resolution, leakage, and reliability properties of cross-spectrum measurements. Three appendices describe applications of cross-spectral analysis to propagation path identification, distant source detection, and time- and frequency-difference-of-arrival estimation.

D. MEASUREMENT METHODS

As explained in Chapter 4, statistical spectral measurements can be obtained from any of a variety of methods, and these various methods are either exactly or approximately equivalent to each other. In principle, the approximations can be made as accurate as desired by choosing sufficiently large provided only that the limit autocorrelation exists. In particular, there are more than 10 alternative methods, which are described by diagrams in Figures 4-1, 4-2, 4-4, 4-6, and 4-7. Because of the fact that all the elements of cross-spectral analysis are straightforward generalizations of the elements of spectral analysis, as explained in Section A, all these alternative methods for obtaining statistical spectra generalize in a straightforward way for statistical cross spectra. Some of these generalizations are briefly described in this section. As explained in Chapter 4, Section A, although the approximations relating the spectra obtained from these various methods can in principle be made as accurate as desired by choosing sufficiently large, it should be emphasized that in applications where must be relatively small, the differences among statistical spectra obtained from different smoothing methods or different windows can he substantial, and the particular choice then becomes an important component of the design problem, as illustrated in Chapter 5,Section D. Although only analog methods are described here, the corresponding digital methods can easily be deduced from these and the digital methods based on the DFT described in Chapter 6, Section C.

F. SUMMARY

In Section A, the elements of cross-spectral analysis are introduced, and it is explained that these are all generalizations of the elements of spectral analysis. These elements include the cross periodogram, cross correlogram, finite-average cross correlation, pseudo-cross spectrum, limit cross correlation and limit cross spectrum, and the various temporally smoothed and spectrally smoothed statistical cross spectra. It is also explained that whereas the limit spectrum gives the mean-square strength of spectral components, the limit cross spectrum gives the correlation of spectral components in two distinct time series. In Section B. the spectral coherence function, which is the spectral correlation coefficient obtained from the limit cross spectrum, is introduced and is shown to be a measure of the degree to which two time-series are related by a linear time-invariant transformation. The two extremes of completely coherent and completely incoherent time-series are described, and the role of coherence in the identification of dynamical systems is explained. Then the concept of coherence is generalized to that of partial coherence for a pair of time-series that are coherent with other time-series. In Section C, the central role of spectral correlation (coherence) in the spectral analysis of random data from periodic phenomena is explained, and the spectral autocoherence function for a single time-series is defined, and is illustrated for a class of amplitude- and phase-modulated sine waves.

In Section D. the various analog methods for statistical spectral analysis that are described in Chapter 4 are generalized for statistical cross-spectral analysis. This includes the methods of temporal and spectral smoothing, Fourier transformation of tapered cross correlations, cross-wave analysis, and cross demodulation (see Figures 7-1, 7-2, 7-3 below). In Section E, the results on resolution, leakage, and reliability that are developed in Chapter 5 for spectral analysis are generalized for cross-spectral analysis, and it is explained that the variability and resolution of cross-spectrum estimates can be even more problematic than for (auto) spectrum estimates.

Appendix 7-1 describes the use of cross-spectral analysis for propagation path identification. Appendix 7-2 explains the use of cross-spectral analysis for distant-source detection. Appendix 7-3 reveals the connection between the cross-correlation function, the cross-spectral density function, and the cross-ambiguity function for the problems of time- and frequency-difference-of-arrival estimation.

Chapter 8, TIME-VARIANT SPECTRAL ANALYSIS

A. GENERAL VARIATION

As explained in Chapter 1, spectral analysis is especially appropriate in principle only for time-invariant linear transformations of data and for data from time-invariant phenomena. But, from a pragmatic point of view, we expect spectral analysis to be useful for time-variant linear transformations and for data from time-variant phenomena, provided that time variation is sufficiently slow. The purpose of this chapter is to clarify why time variation must be slow and how slow it must be. Only the situation in which the time-series data alone is to be used for spectral analysis is considered. That is, the model-fitting methods described in Chapter 9, which typically require additional information for the purpose of model-type selection, are omitted from consideration.

1. The Physical Spectrum

Regardless of the phenomenon or the data under study, the time-variant periodogram introduced in Chapter 2, Section A, is the normalized squared magnitude of a time-variant density of spectral components (namely, the time-variant finite-time complex spectrum; see (2b) in Chapter 2), and is therefore the most natural definition and the only generally appropriate definition of a nonstatistical time-variant spectrum. As explained in Chapter 5, Section C, if there is no ensemble of time-series available from the phenomenon of interest, then the degree of randomness of this spectrum can be reduced (reliability increased) only by temporal or spectral smoothing, with the result that temporal and spectral resolution are severely constrained by Grenander’s uncertainty condition, (89) in Chapter 5,

(1)  

which is a necessary and sufficient condition (for a broad class of time-series data) for high reliability. Thus, the reliable resolvability of time variation in spectral characteristics of a phenomenon is limited by a temporal resolution width that must greatly exceed the reciprocal of the spectral resolution width . On the other hand, if an ensemble of replicas of a time-series (not timetranslates of a single time-series but rather genuine random samples as would be obtained, for example, from replicating an experiment) from a given timevariant phenomenon is available, then as explained in Chapter 5, Section A, the degree of randomness can be reduced by ensemble averaging with no degradation in either temporal or spectral resolution. Thus, resolvability is limited by only Gabor’s uncertainty principle, (88) in Chapter 5,

(2)  

which applies to the time-variant periodogram, whether or not it is ensemble averaged. Furthermore, even when an ensemble is not physically available, the concept of an ensemble-averaged time-variant spectrum can be of value.¹ Specifically, the idealized limit of an ensemble-averaged time-variant periodogram, (4) in Chapter 5, which is the expected time-variant periodogram

(3)  

can be interpreted as a completely reliable (zero degree of randomness) measure of the time-variant spectral characteristics of a phenomenon. This most reliable measure exhibits the best possible temporal and spectral resolutions, that is, the resolutions satisfy (2). From this point of view, it apparently makes no sense to conceive of or seek a probabilistic measure of time-variant spectral characteristics that exhibits finer resolutions than those that satisfy (2).

Nevertheless, there is a probabilistic function of time and frequency that plays a fundamental role in the mathematical characterization of the expected periodogram and that is not subject to any counterpart of (2). Specifically, it can be shown (exercise 1) [Mark 1970], that the expected periodogram is a time- and frequency-smoothed version of a function called the probabilistic instantaneous spectrum,

(4)  

in which the smoothing function is defined by

(5)  

and the probabilistic instantaneous spectrum is defined by

(6)  

(7)  

where is called the probabilistic instantaneous autocorrelation function. Although the probabilistic instantaneous spectrum can in principle be measured as accurately as desired when a sufficiently large ensemble is physically available, in general it does not represent a time-variant spectrum of the data in any physical sense.² It can only approximate a time-variant spectrum, and this approximation can be close only when the time-variation is sufficiently slow that the fine structure of the function is accurately resolved with resolution widths satisfying

(8)  

(see [Mark 1970; Donati 1971]). But it can be shown by using (4)-(5) that when (8) is satisfied, then (using )

(9)  

As a reflection of the facts stated in the preceding discussion, the expected time-variant spectrum is called the physical spectrum to distinguish it from the generally nonphysical instantaneous probabilistic spectrum [Mark 1970; Eberly and Wodkiewicz 1977].

===============

¹ Wold’s isomorphism cannot be used to envision an appropriate ensemble in this case, as done in Chapter 5, Section B for time-invariant phenomena, because the equivalence between ensemble- and time-averaging would result in all time variation being averaged away by the ensemble averaging operation.

² However, it is explained in Part II that for a cyclostationary or almost cyclostationary process, the Fourier coefficients of the periodic or almost periodic function are spectral correlation functions, which do indeed have a concrete physical interpretation.

C. SUMMARY

In Section A the fundamental limitations on the simultaneous temporal and spectral resolution capabilities of statistical spectra are described, and the advantage of ensemble averaging (when possible) is explained. The instantaneous probabilistic spectrum is introduced and its relation to the physical spectrum is explained and illustrated with an application to the problem of identification of a time-variant linear system. An alternative to the instantaneous probabilistic spectrum as an idealized probabilistic time-variant spectrum, called the evolutionary spectrum, is introduced and its direct relationship with the system function is explained. The limitations on measurement of these idealized probabilistic spectra, when ensemble averaging cannot be used, are explained and the concepts of locally stationary and locally ergodic processes are introduced.

In Section B the fact that a periodically time-variant phenomenon is an exceptional case is briefly discussed. It is explained that for this special type of time-variant phenomenon, the fundamental resolution limitations do not apply. Another exception also should be mentioned: those situations in which the spectral analyst has more information about the phenomenon under study than can be obtained from the time-series alone. For example, if it is known that the time-series can be accurately modeled as an autoregression, then—as explained in Chapter 9—spectral resolution performance that exceeds that of the periodogram is possible (but is not guaranteed).

A general treatment of the related problem of reliable measurement of time-variant auto- and cross-correlation functions is given in [Gardner 1987c].

Chapter 9, PARAMETRIC METHODS

A. INTRODUCTION

All the methods of spectral analysis described in previous chapters are based on a direct decomposition of the data to be analyzed into spectral components using Fourier transformation or filtering and are therefore called direct methods. In contrast, the methods studied in this chapter are based on an entirely different philosophy. Specifically, each of these methods fits a particular form of model to the data by adjusting the values of parameters in the model. Once the model fitting is complete, the parameter values can be substituted into a formula to obtain the limit spectrum for that model with the estimated parameter values. There are many variations on this prototypical method. All such methods are referred to as parametric methods, whereas the direct methods described in previous chapters based on direct decomposition into spectral components are referred to as nonparametric methods.

Parametric methods of spectral analysis can yield better resolution of multiple spectral lines or other narrow features, particularly if they are close together in frequency, when the amount of data is severely limited, especially if the data-segment length is smaller than the reciprocal of the desired spectral resolution, and the experiment is repeatable so that an ensemble of data segments is available. (This occurs, for example, in some sensor-array signal-processing problems, where the spatial data-segment length is the number of sensors and ensemble averaging is performed by time-averaging.) But more generally the relative advantages depend on the appropriateness of the form of the model chosen. In some cases, nonparametric methods are helpful in selecting a form of model to be used as the basis for a parametric method. In fact, in some applications the main objective is to fit a model to the data, and nonparametric spectral analysis methods are often used as a first step. But, even when an appropriate form of model for a signal is known, if the signal is masked by noise, then nonparametric methods can be superior for spectral analysis. However, parametric methods can be particularly useful for identification (detection and estimation) of additive sine wave components to be removed (to minimize spectral leakage) before application of a nonparametric method. Generally speaking. parametric methods are more computationally burdensome than nonparametric methods, but some methods based on autoregressive models are computationally competitive with direct methods based on the FFT. The practicality of autoregressivemodel-fitting methods of spectral analysis is attested to by the wide range of problems to which these methods have been applied. These include radar, sonar, image processing, radio astronomy, biomedicine, speech analysis and synthesis, geophysics, seismology, and oceanography.

Since parametric methods of spectral analysis are diverse and often tailored to special types of data, it is not possible to present a comprehensive and unified treatment paralleling that presented in previous chapters for the direct methods. However, the fundamental concepts and mathematical theory underlying the particularly important class of autoregressive methods can be and therefore are presented in a unified manner. In keeping with the philosophy of this book, the unified treatment is non-probabilistic, whereas other treatments of the same material are typically couched within the conventional probabilistic framework. This is possibly the first time a unified theoretical treatment of this class of methods, without the use of the abstract stochastic process framework, has been presented.

Although the results of the fraction-of-time probabilistic analysis, such as bias and variance formulas derived in Chapter 5, apply to all direct methods, the parametric methods are not amenable to such straightforward probabilistic analysis—fraction-of-time or stochastic. Useful results on bias and variance are typically obtainable only asymptotically as the data segment length used for spectral analysis approaches infinity (see [Kay 1987]), and such results have typically been derived only within the abstract stochastic process framework for no special reason I can discern other than ignorance of the fraction-of-time theory presented in the book [Bk2] and now this website.

In Section B, the non-stochastic theoretical background for autoregressive and related ARMA methods is presented. Then, in Sections C and D some of the methods that have proven to be of practical value are described. Finally, in Section E, an extensive experimental study and comparison of these and direct methods is presented. The reader is cautioned that the term non-probabilistic used frequently in this chapter and elsewhere in the book, usually means non-stochastic. In many cases of this usage herein, the quantities or modeling methods referred to are based on time averages but admit a fraction-of-time probabilistic interpretation as explained in Chapter 5.Thus, strictly speaking, they are temporally-probabilistic but non-stochastic. This point is often a conceptual stumbling block for readers who are familiar with the conventional stochastic-process theory and are looking for a flaw in this author’s thinking that would justify their dismissal of the alternative theory presented herein despite its considerable advantages. Unfortunately, such biased readers all too often appear to think they’ve found a flaw and believe this author has resorted to slight-of-hand to dismiss troublesome aspects of the non-stochastic approach. This author writes extremely carefully and the likelihood of their being flaws in the logic or any devious methods of tricking the reader is near zero.

C. AUTOREGRESSIVE METHODS

6. Discussion

All the direct methods of spectral analysis described in preceding chapters yield spectrum estimates of the MA type except for the minimum-leakage method, which yields spectrum estimates of either the AR or ARMA types and generally provides better resolution of sharp spectral peaks. It has been reported that of the four AR LS methods, the best resolution of sharp peaks using short data-segment lengths is provided by the FB method, the poorest (relatively speaking) is provided by the YW method, and the Burg method does somewhat better than the covariance method. But there are many other performance criteria to be considered when selecting a method in practice. For example, both the YW and Burg methods guarantee a stable AR model, whereas neither the covariance nor FB LS methods guarantee stability, although in practice they typically do yield stable models, and even an unstable model can produce a useful spectrum estimate. The variance of the minimum-leakage AR method is reportedly smaller than that of the YW method [Baggeroer 1976], but the YW method has smaller variance than both the covariancc method and the Burg method for short data segments; the FB LS method has been said to have the smallest variance (as well as the best resolution) of all the LS AR methods [Swingler 1974; Ulrych and Bishop 1975; Nuttal 1976; Ulrych and Clayton 1976] but the minimum-leakage method can be superior as illustrated in Section E. Also, for sine waves in additive broadband noise, the YW, covariance, and Burg methods all occasionally produce two close spectral peaks around the frequency of a single sine wave (the spectral line-splitting phenomenon), but the FB LS method [Kay and Marple 1981] and the modified (weighted) Burg method [Helme and Nikias 1985], [Paliwal 1985] have not been observed to do this. Moreover, the location of the peaks in these latter two methods are generally closer to the correct frequencies than in the other three LS AR methods [Kay 1987]. It is also of interest that in all four LS AR methods, the amplitude of a spectral peak is proportional to the square of the power in the underlying spectral line associated with a sine wave for high signal-to-noise ratio, but the area under the peak is proportional to the power (because the width is inversely proportional to the power) [Lacoss 1971]. On the other hand, the amplitude of a spectral peak produced by the minimum-leakage AR method is indeed proportional to the power [Lacoss 1971] (assuming that the width of the spectral line is narrower than the effective resolution width for this method) as it is for all the direct methods. In summary, it appears that the best performing LS AR methods for sharply peaked spectra are the FB LS method and the modified Burg method. It should also be noted that additive white noise in the data generally has a smoothing effect on these AR spectrum estimates. Consequently, for sufficiently low signal-to-noise ratio sine waves in noise, the resolution performance of all these LS AR methods becomes inferior to that of the direct methods [Kay 1987]. (Also, for MA-type time-series, AR methods can be substantially inferior to direct methods [Beamish and Priestley 1981].) Nevertheless, other AR methods, such as the ODNE and SVD methods can reportedly provide improved performance for some low signal-to-noise ratio (e.g., as low as 0 dB) applications [Cadzow 1982; Tufts and Kumaresan 1982; Cadzow et al. 1983]. These SVD methods also considerably improve on other related but earlier parametric methods designed specifically for sine waves in noise, such as the Hildebrand-Prony method and the Pisarenko method (see [Tufts and Kumaresan 1982; Kay 1987]).

Another performance criterion to consider in selecting a method for spectral analysis is the ease with which spectrum estimates can be updated as time passes in applications where it is desired to do time-variant spectral analysis. Updating is relatively straightforward for direct methods, as explained in Chapter 6, and is also possible for many of the AR methods but is not quite as simple [Friedlander 1982a, 1982b, 1983a, 1983b; Cioffi and Kailath 1984; Honig and Messerschmitt 1984; Marple 1987]. It should be emphasized that the focus on computationally efficient methods of spectral analysis is appropriate in situations where large amounts of data are continually produced, such as in radar, sonar, and seismology signal-processing applications. However, in situations where the cost or other limitations on collecting data are dominant, this focus is not necessarily appropriate, and the more computationally burdensome but potentially higher-performing exact or near-exact maximum-likelihood methods can be attractive. This is especially true for ARMA methods, which are discussed in the next section.

Finally, it should be emphasized that the appropriateness of parametric methods for sharply peaked spectra applies only when there are multiple peaks that are closely spaced. If the separation between peaks exceeds the resolution width determined by the amount of data available, then direct non- parametric methods typically perform just as well, if not better. In fact it is shown in exercise 22 that for a spectrum with a single sharp peak, modeled by a time-series consisting of a single sine wave in additive white Gaussian noise, the periodogram provides optimum (maximum-likelihood) estimates of the amplitude and frequency of the sine wave. Furthermore, for multiple sine waves with frequency separation sufficiently in excess of , the periodogram is still nearly optimum. However, when there are multiple spectral peaks spaced more closely than , the parametric methods can perform better than the direct methods. If the complex spectrum obtained from the DFT with substantial zero-padding is used to estimate (phase as well as frequency and amplitude) and subtract sequentially each of a multiplicity of additive sine wave components, and the spectrum of the residual is then estimated by direct methods, then performance can be considerably improved, but is still not comparable with parametric methods for data consisting of multiple closely spaced sine waves in additive noise. Furthermore, parametric methods typically provide substantial improvements in performance relative to direct methods for sensor-array signal-processing problems that arise in radar, sonar, and seismology applications. The reason for this is that in these problems, the number of spatial samples is very small, but the correlation matrix for these samples can be relatively accurately estimated (since the number of products averaged is not restricted by but rather is determined by the number of time samples taken at each of the sensors). Thus, the problems of energy-source detection and direction-of-arrival estimation, which are the spatial analogs of the temporal counterparts of spectral-line detection and spectral-line-frequency estimation, can benefit from exploitation of special structure in the correlation matrix, including AR structure and special eigenstructure that can be revealed by singular value decomposition.

F. SUMMARY

In Section B, the theory of autoregressive modeling of time-series, which underlies many of the parametric methods of spectral analysis, is presented in a concise but thorough form. This includes the topics of Yule-Walker equations, Levinson-Durbin algorithm, linear prediction, Wold-Cramer decomposition, maximum-entropy model, Lattice filter, and Cholesky factorization. Then in Section C, after a general discussion of the relative merits of AR, MA, and ARMA modeling, the theory of autoregressive modeling is exploited in a step-by-step development of the most popular AR model-fitting methods for spectral analysis. These include 1) the Yule-Walker (or autocorrelation type of least squares linear predictive) method and its interpretations in terms of maximum-entropy and autocorrelation extrapolation; 2) the covariance type of least squares method and its improved forward-backward linear predictive version, and 3) the lattice-constrained variant of this, known as the Burg method; 4) the overdetermined-normal-equations variation on the least squares linear predictive methods (autocorrelation and autocovariance types), and 5) two modifications based on singular value decomposition of the data-correlation matrix; and 6) the maximum-likelihood approach. Also, four model-order-determining methods, known as final prediction error, information criterion, autoregressive transfer-function criterion, and singular-value-decomposition, are described. The subsection on AR model fitting concludes with a comparative discussion of the relative merits of these various methods. In Section D, the many methods for ARMA model fitting are classified into three primary groups. The group that includes the most computationally attractive methods is then focused on, and the extended and modified Yule-Walker equations, which form the basis for these methods, are derived. It is explained that most of the AR methods can be simply adapted to the task of estimating the AR parameters in the ARMA model, and an adaptation of the ODNE-SVD method is described. Then a variety of methods for utilizing the AR estimates, together with the autocorrelation estimates or the data, to estimate the MA parameters are described. These include (1) direct methods preceded by an inverse AR filtering operation on the data, (2) a variation on the Blackman-Tukey and Wiener-Daniell versions of this approach that circumvents the data-filtering operation, (3) another variation that utilizes forward-backward filtering, (4) Shanks’ method, which is based on a decomposition of the spectrum into causal and anticausal parts, and (5)a variation on this that uses the overdetermined-equations technique. The chapter concludes with an extensive experimental study that compares and contrasts the performances of many of the methods described herein.

As with all theory and method presented in this book, there is no reliance in this chapter on the abstract stochastic process data models typical of all studies performed since around 1970. Such abstraction offers nothing beyond the more concrete approach presented here, but does cost readers a deeper understanding of the relationship between theory and practice.